Cylindre de révolution

CYLINDRE DE RÉVOLUTION
Cylinder of revolution, Drehzylinder

Équation du cylindre de rayon R d'axe (O, ) avec

.
Pour obtenir l'équation du cylindre d'axe (AB) et passant par C, écrire

.
Équation cylindrique réduite :

.
Équation cartésienne :

.
Paramétrisations cartésiennes :

(cf figure de droite).
Quadrique développable.
Première forme quadratique fondamentale :

.
Élément d’aire :

.
Deuxième forme quadratique fondamentale :

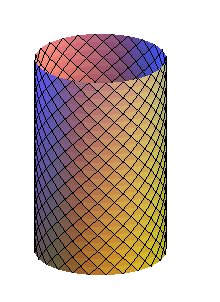Paramétrisation dont les lignes de coordonées forment un double réseau d'hélices circulaires orthogonales, qui sont aussi les loxodromies à 45° de ce cylindre (qu'il soit placé verticalement ou horizontalement).

Le cylindre de révolution est la surface engendrée par la révolution d’une droite parallèle à un axe, autour de cet axe.
On peut développer le cylindre en faisant correspondre au point M le point du plan de coordonnées cartésiennes .

Courbes remarquables tracées sur le cylindre de révolution :
- lignes de courbure : les cercles z = cte et les génératrices.
- géodésiques, hélices et loxodromies : les cercles z = cte, les génératrices, et les hélices circulaires.
- cercles géodésiques.
- pseudo-géodésiques.

Animation de l'enroulement d'une feuille de papier carrée de côté L en un cylindre.
Paramétrisation : 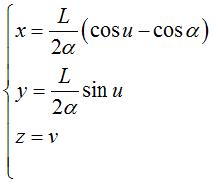avec , , pour allant de 0 à .

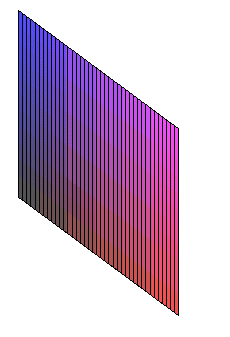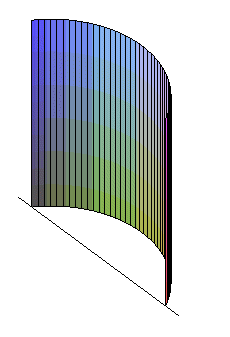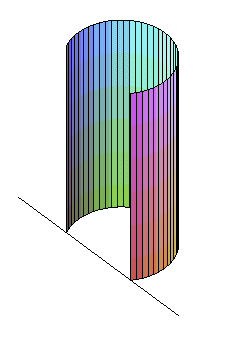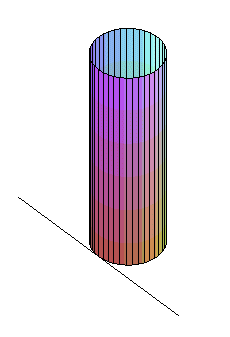Voir aussi les courbes cylindriques, les équidomoïdes, les solides de Steinmetz (exemple ci-dessous), le pliage d'un cylindre de révolution en papier.

Intersection de 3 cylindres orthogonaux, par Alain Esculier

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres