Notion étudiée par Catalan en 1843 (J. E. P.,1843, 29e cahier, p.121-156), Delaunay en 1843 ( J. M.,1843, t. 8, p. 231-244), Darboux en 1883 (C. R.,1883, t.96, p.54) , et Whittemore en 1901. Voir aussi  [Blaschke p. 99] , un article sur le sujet dans le bulletin de l'APMEP.

 

Equation différentielle (def 1) pour une surface , avec les notations classiques: : .

La notion de cercle géodésique est la généralisation à une surface quelconque de celle de cercle dans le plan.

Il existe deux définitions principales, non équivalentes en général :

DEF 1 : lieu des points de la surface situés à une distance géodésique (le rayon géodésique) donnée d'un centre situé sur la surface ; par distance géodésique, on entend : distance suivant une géodésique, distance qui peut ne pas être la plus courte possible.
 

DEF 2 : courbe maximale à courbure géodésique constante non nulle - le cas de la courbure nulle donnant les (droites) géodésiques. Le rayon de ce cercle géodésique est alors l'inverse de cette courbure. Autrement dit, la sphère qui contient le cercle osculateur de la courbe et dont le centre est dans le plan tangent à la surface a un rayon constant. De façon imagée, cette définition correspond aux trajectoires d'observateurs se déplaçant sur la surface en tournant à gauche ou à droite d'un angle constant, ou de petites voitures dont la direction est bloquée dans une position fixée. Nota : les cercles géodésiques ne sont pas en général des cercles gauches (qui sont, eux, à courbure, tout court, constante).

Whittemore a démontré que les deux définitions coïncident pour les surfaces à courbure de Gauss constante, qui sont les surfaces applicables sur un plan (autrement dit, développables), une sphère, ou une pseudo-sphère.
Delaunay a démontré que, comme dans le plan, les courbes fermées de plus petite longueur renfermant une aire donnée, ou de longueur donnée et renfermant la plus grande aire sont des cercles géodésiques au sens numéro 2 (propriété isopérimétrique).
D'après le lemme de Gauss, les cercles géodésiques (définition 1) de centre donné sont les trajectoires orthogonales sur la surface des géodésiques issues de ce centre [Pressley p. 245].

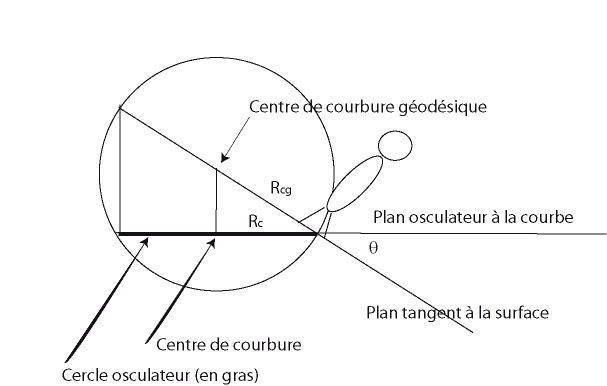
Exemples :
     - les cercles géodésiques du plan ou de la sphère sont les cercles habituels mais on verra ci-dessous qu'ils ont de nombreux rayons différents !

Cercle parallèle de colatitude  sur la sphère de rayon a :  - en temps que cercle "normal" il a pour rayon . - avec la définition 1, il a deux centres N et S, et deux rayons  et . - avec la définition 2, son centre  est le point du plan tangent à la sphère qui se projette sur le plan du cercle au centre "normal" de ce cercle, et son rayon est donc .  L'équateur a pour rayon  avec la définition 1, et  avec la définition 2 (c'est une géodésique).

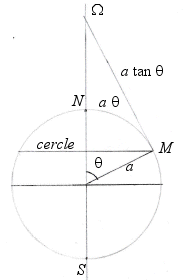    - un cercle (au sens classique) d'une surface n'en est, en général, pas un cercle géodésique !
 

Exemple de la surface  (vue du milieu) ; les deux cercles rouges ont une courbure constante (par def !) mais n'ont pas une courbure géodésique constante puisque le plan tangent ne fait pas un angle constant avec le plan des cercles. La def 2 n'est pas vérifiée, et la 1 non plus. Exemple de la surface  (à droite) ; le plan tangent fait cette fois un angle constant (nul) avec le plan des cercles, donc ce sont des cercles géodésiques pour la def 2, mais non pour la def 1...

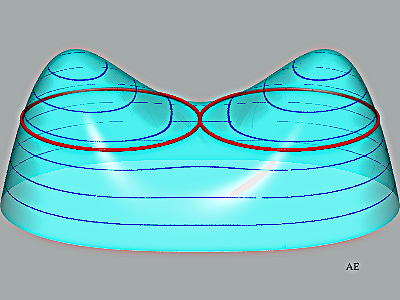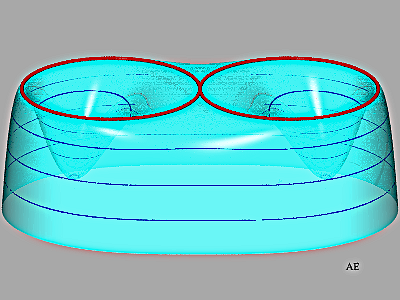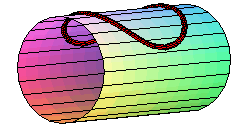
    - les cercles géodésiques (def 1 ou 2) d'un cylindre ou d'un cône, et plus généralement des surfaces développables sont les courbes qui se transforment en des cercles quand on applique la surface sur un plan ; concrètement, on peut imaginer le cercle géodésique comme le bord d'une crêpe circulaire appliquée sur la surface, crêpe qui peut éventuellement se recouvrir elle-même. Le rayon géodésique est les rayon du cercle développé.

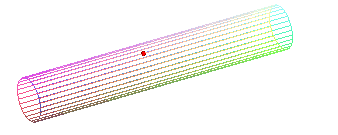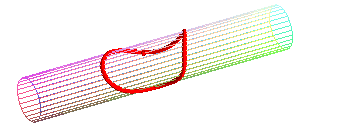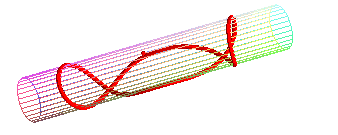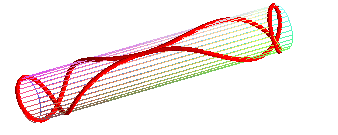
Cas particulier du cylindre de révolution :

Paramétrisation pour un cercle géodésique de rayon b sur un cylindre de rayon a : . Il possède des points doubles dès que son diamètre est supérieur à la circonférence du cylindre (). Comparer avec la courbe de la crêpe.		Lorsque son rayon est égal à la circonférence du cylindre, le "cercle" passe par son centre...
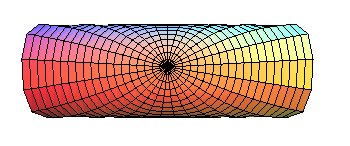
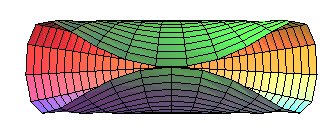
Paramétrisation du cylindre par les coordonnées géodésiques polaires, dont les lignes de coordonnées sont des hélices circulaires et des cercles géodésiques : .

Cas particulier du cône de révolution :

Paramétrisation pour un cercle géodésique de rayon b, de centre situé à une distance a du sommet d'un cône de demi-angle au sommet  :  Remarque : pour u fixé et b variable la formule ci-dessus donne les géodésiques issues du centre du cercle. Voir le cas particulier a = b sur la page du cône de révolution.

Animation pour un cercle de rayon allant de 0 à 2a.

A l'arrivée de l'animation précédente, le cercle passe par son centre. Sont tracées quelques géodésiques issues du centre (point jaune).

 
 

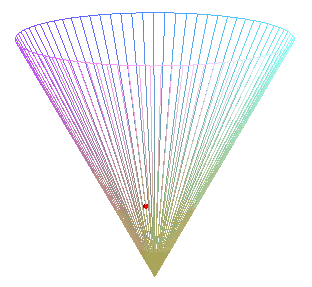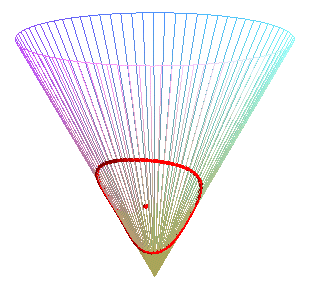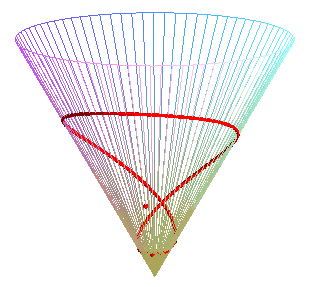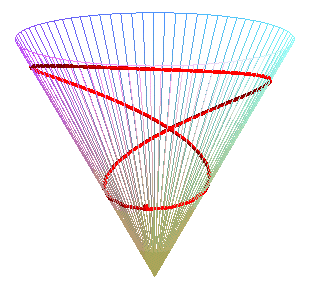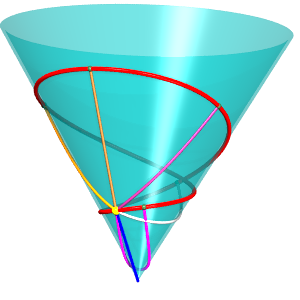Un cas où les deux définitions ne sont pas équivalentes : le paraboloïde hyperbolique équilatère. Sont tracées sur cette figure les géodésiques issues de O et les points à distance géodésique données de O, figurant les cercles géodésiques de la définition 1. On constate par le calcul que la courbure géodésique n'est pas constante le long de ces cercles. Figures réalisées avec Rhinocéros par Robert March.
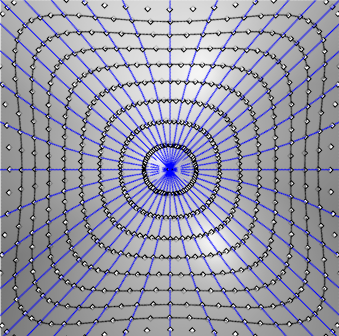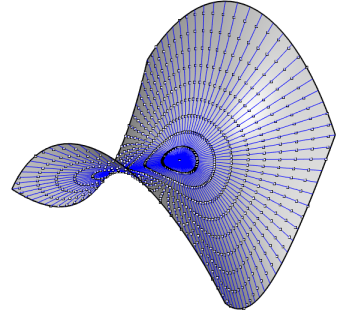Autre exemple : la selle pour singe.
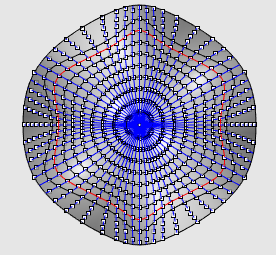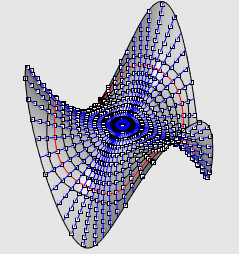Troisième exemple : le tore (voir aussi la page spécifique sur les géodésiques).

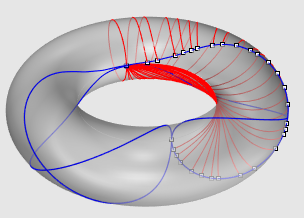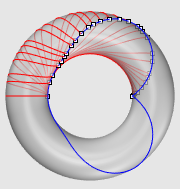Ont été aussi définies les ellipses/hyperboles géodésiques, lieux des points dont la somme/différence des distances géodésiques à deux points fixes est constante. Pour le cas de la sphère, voir cette page.
Autre exemple : les lignes de courbure de l'ellipsoïde sont les ellipses géodésiques de foyers les ombilics.
 
 

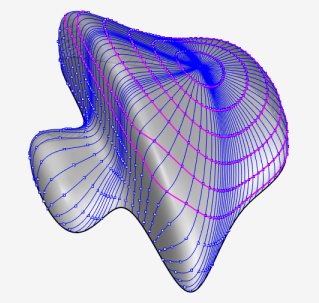
Des "cercles" avec des portions rectilignes....

Napperons mexicains : des cercles développables....

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2018