Notion étudiée par Bobillier en 1829. Voir  : Paul Appell : cours de mécanique rationnelle, page 220.

 

Équation différentielle : , où  est le vecteur normal à la surface.

Les chaînettes d'une surface sont les lignes d'équilibre d'un fil pesant infiniment mince, homogène, flexible et inextensible inclus dans la surface, en présence d'un champ de pesanteur uniforme.

Les chaînettes sont aussi les courbes minimisant l'altitude du centre de gravité, à savoir que la chainette de longueur l  joignant A à B est parmi les courbes homogènes de longueur l joignant A à B tracées sur la surface, celle dont le centre de gravité est le plus bas.

Voici la provenance de l'équation différentielle ci-dessus :
 

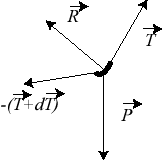
La relation fondamentale de la statique appliquée à un élément de fil s'écrit ( = tension du fil en M,  = poids,  = réaction normale de la surface) , ce qui donne : (1)  (m = masse linéique du fil,  = vecteur tangent à la courbe). Or en utilisant les formules de Binet :  où  est le vecteur normal à la courbe. En multipliant l'égalité  par , on obtient alors , soit , d'où  ; en reportant la valeur de T dans (1), on en déduit l'équation différentielle.

Exemples :

    - les chaînettes d'un plan non horizontal sont les chaînettes habituelles.

    - les chaînettes d'un cylindre vertical quelconque sont les courbes se développant en des chaînettes d'axe vertical.

    - les chaînettes cylindriques

    - les chaînettes coniques

    - les chaînettes sphériques
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2004