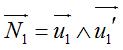Notion étudiée par Fuchs et Tabachnikov en 1999 [More on paper folding, The American Mathematical Monthly, 106, p. 27-35], et par Pottmann et Walner en 2001 [Computational Line Geometry, Springer, 2001, p 416-422] Voir aussi Folding Curves, par Robert Geretschläger.

Lorsque deux surfaces développables contiennent une même courbe, et que cette courbe a même courbure géodésique en tout point par rapport aux deux surfaces, les plans tangents aux deux surfaces forment le même angle avec le plan osculateur à la courbe, en tous points de celle-ci et sont donc soit égaux, soit symétriques par rapport à ce plan.

Rappelons que la courbure géodésique est la courbure de la courbe obtenue en développant la surface. Si donc l'on plie une feuille de papier cartonné le long d'une courbe gauche, on obtient de part et d'autre de la courbe deux surfaces développables ayant la propriété précédente. Si la première surface est connue, la deuxième est définie de façon unique par le fait qu'elle est l'enveloppe des symétriques des plans tangents à la première par rapport aux plans osculateurs le long de la courbe.
 
 

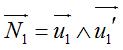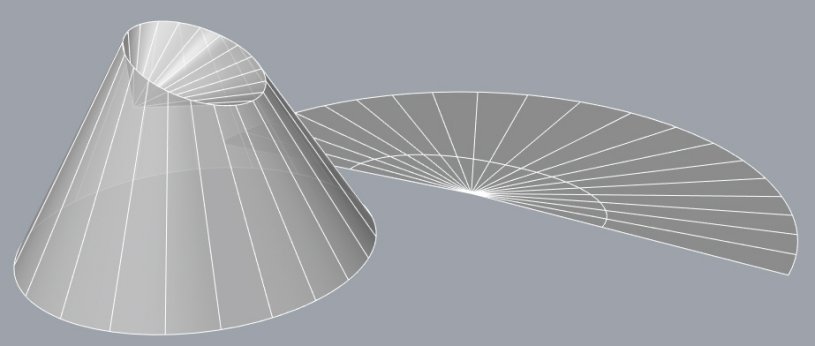
Si la courbe de la pliure est engendrée par le point , et la génératrice de la première nappe est dirigée par , on obtient le vecteur directeur  de la deuxième nappe en calculant , ,  où  est la réflexion par rapport au plan orthogonal à  ; on a alors .

 

Exemple : si la pliure est plane, la partie pliée est la nappe symétrique par rapport au plan de celle-ci. Ci-contre, cas d'un cône et d'un cylindre parabolique.

Formules dans le cas d'une pliure dans un cylindre de révolution :
 

Cylindre , courbe de la pliure : . Les génératrices de la partie pliée ont pour vecteur directeur : .   Pour une pliure plane : ,  : la partie pliée est le cylindre de révolution symétrique par rapport au plan de la pliure. Pour une pliure courbe de Viviani : , . Pour une pliure pseudo-géodésique : , . Par définition, l'angle entre le plan osculateur et le plan tangent à l'une ou l'autre surface est constant, égal à .

 

Expérience concrète avec du papier fort. A droite, ensacheuse col de cygne. Vidéo sur youtube.

 

Modélisation mathématique de l'enroulement du cylindre. Les génératrices de la partie pliée ont ici une longueur constante, et ne modélisent donc pas la feuille de papier rectangulaire. Noter qu'à mi-parcours, le pli est plan, et que donc la partie pliée est le demi-cylindre symétrique. Paramétrisation de la partie cylindrique :,  avec t entre  et , u entre 0 et 1, et l'animation de = 0,001 à .

Images de Robert March.

 

Lien vers de superbes réalisations en papier virtuel plié.

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2019