SURFACE DE DINI
Dini's surface,
Dinische Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE DINI
Dini's surface,
Dinische Fläche
| Surface étudiée par Dini en 1865.
Ulisse Dini (1845-1918) : mathématicien italien. Autres nom : hélicoïde de Dini, hélicoïde pseudosphérique. Lien : catalogue des modèles de l'université de Besançon. |
Paramétrisation cartésienne :  ( )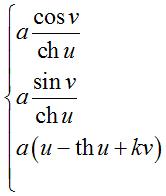
; cf. d'autres paramétrisations à partir de celles de la
tractrice).
Première forme quadratique fondamentale :  .
Courbure de Gauss :  . |
| La surface de Dini est la surface engendrée par
le vissage d'une tractrice
le long de son asymptote, autrement dit, l'hélicoïde
de génératrice une tractrice et d'axe l'asymptote de cette
tractrice.
Sa propriété principale est d'être à courbure totale constante, comme la pseudosphère engendrée, elle, par la rotation d'une tractrice autour de son asymptote. Une autre propriété est d'être le seul hélicoïde dont les lignes de courbures sont les méridiennes (théorème de Bianchi, cf. [gray] p. 483). Ci-contre, rotation autour de son axe d'une demi-surface de Dini, et modèle en plâtre issu de ce site. |
 |
 |
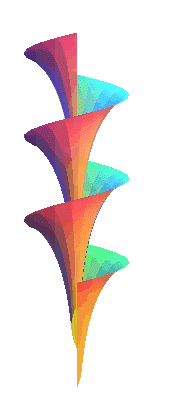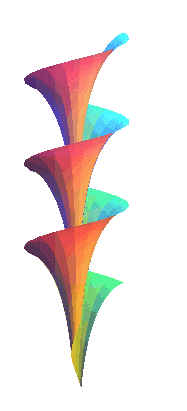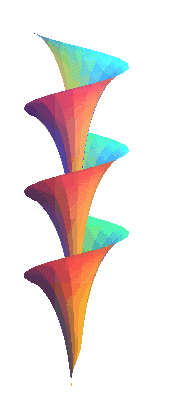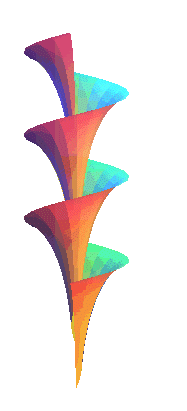Voir aussi la surface de
Kuen, autre surface à courbure négative constante.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2018