Cartesian parametrization:
Cartesian equation: eliminate u between
Polar equation of the section by a plane z = h:
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CYCLOTOMIC SURFACE
| Surface studied by Eugene Catalan in 1859; name proposed by Barre de Saint Venant.
From the Greek kuklos: "circle" and temnein "cut". |
| Spherical equation for a cyclotomic surface with axis Oz and directrix with polar equation Cartesian parametrization: Cartesian equation: eliminate u between Polar equation of the section by a plane z = h: |
A cyclotomic surface is a circled surface generated by a circle with varying radius in rotation around one of its diameters (its center O remaining fixed).
The surface is completely defined by the point O and the section of the surface by the plane passing through O and perpendicular to the fixed diameter of the generating circles, such section is called the directrix of the surface.
Examples:
If the directrix is a circle with center O, then the associated cyclotomic surface is the sphere.
If the directrix is a circle passing by O:
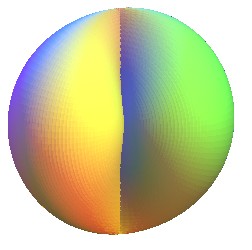 |
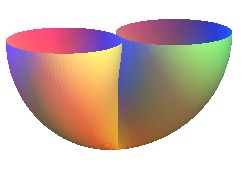 |
Spherical equation: Cartesian equation: Quartic surface. Polar equation of the section by a plane z = h: Volume : Area: |
If the directrix is a line that does not pass by O:
 |
 |
Spherical equation: Cartesian equation: Quartic surface. |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017