FINITE RIEMANN'S MINIMAL SURFACE
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
FINITE RIEMANN'S MINIMAL SURFACE
| Surface studied by David Hoffman and Hermann Karcher
in 1993.
Links: virtualmathmuseum.org/Surface/lopez-ros/lopez-ros.html minimal.sitehost.iu.edu/research/claynotes.pdf p 29 |
Cartesian parametrization: 
with  .
the views on this page are made with k = 3/10. |
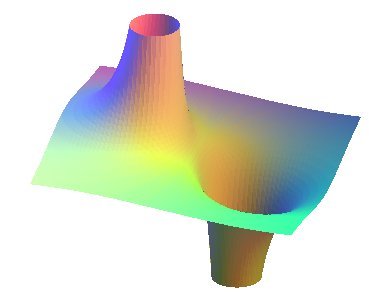
The Riemann finite minimal surface is the minimal
surface obtained by taking 
(and then 
)
in the Weierstrass parametrization of a minimal
surface: 
.
It has two infinite sheets of the type of those of the
catenoid
and an infinite sheet with an asymptote plane (hence the name "finite",
as opposed to Riemann's original
minimal surface that has an infinite number of plane sheets).
Note that if extended, the sheets intersect, contrary
to those of Costa's surface.
The Riemann finite minimal surface has the same shape
as the cubic surfaces with equations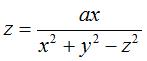 
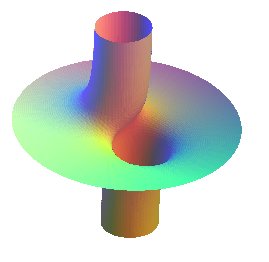
and  .... |
asymptote cylinder x²+y²=a² |
|
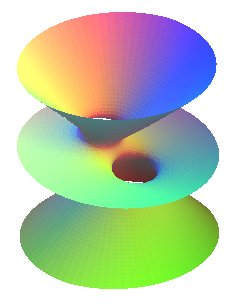
... or as the sextic surface with equation  ,
as well as the transcendental surface with equation  .
For both of them, the asymptote lines are the straight lines  . |
 |
 |
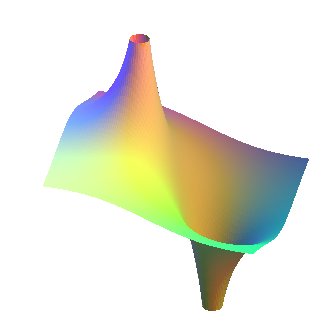A Riemann finite surface, by Alain Esculier. |
A Riemann finite surface in wire, by Christoph Soland, Bugnon gymnasium, Lausanne, see at Dyck's surface. |
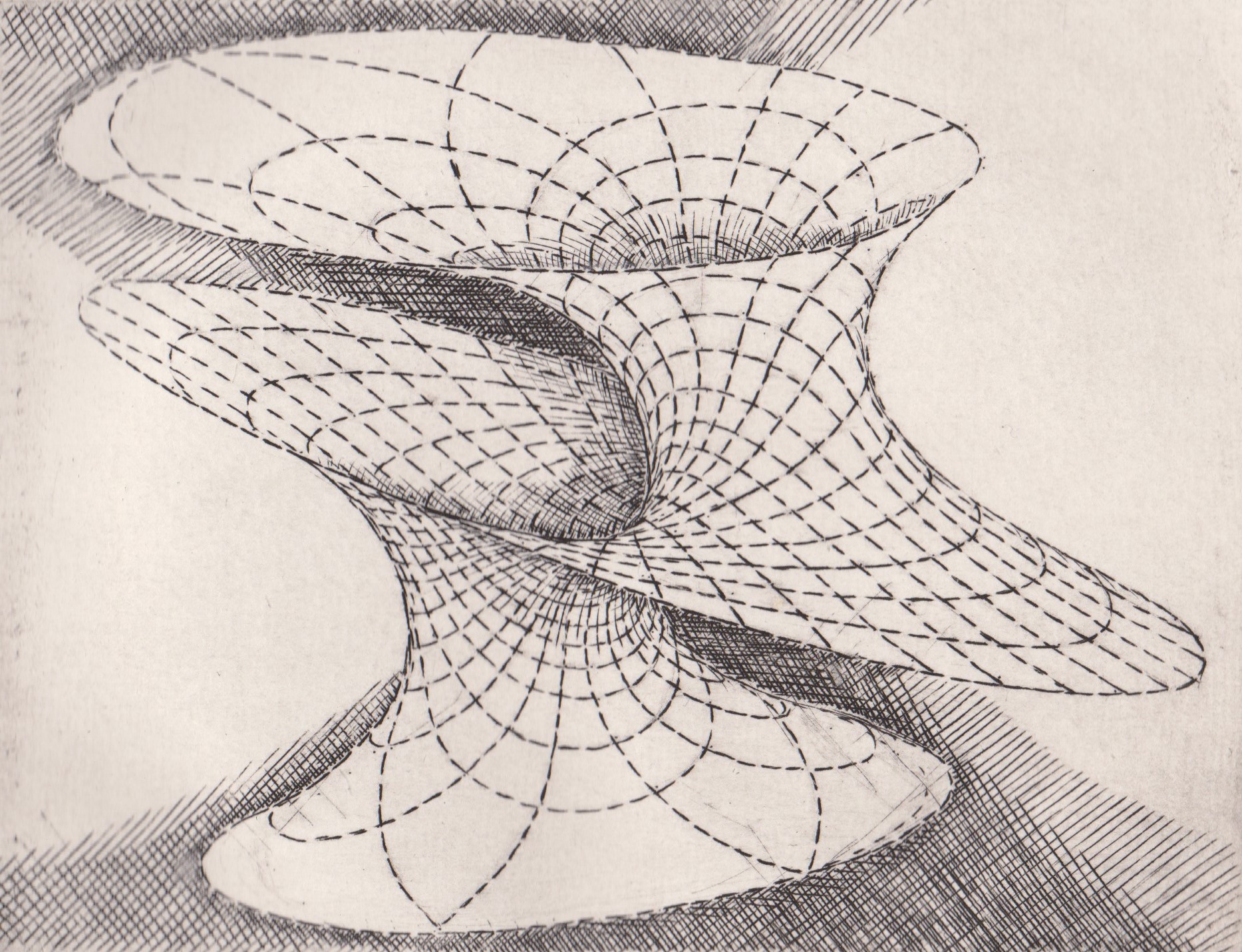
Engraving of this surface, by Patrice Jeener
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017