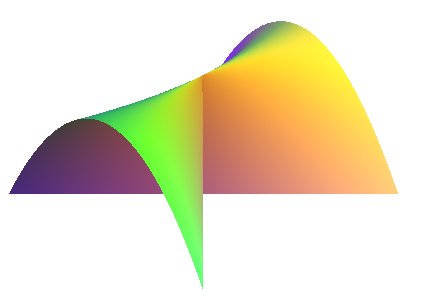
Cartesian equation: . Ruled cubic surface. Cylindrical equation: . Cartesian parametrization:  or  (). The parametrization "forgets" the lower part of the axis Oz that is part of the algebraic surface, and constitutes the handle of the umbrella....

Whitney's umbrella is a right conoid with directrix a parabola with axis parallel to its axis; it is therefore a parabolic conoid.
It is a surface that crosses itself along a half-line (here, Oz) the ends of which are cuspidal points or Whitney singular points (one of them at infinity).
 
 

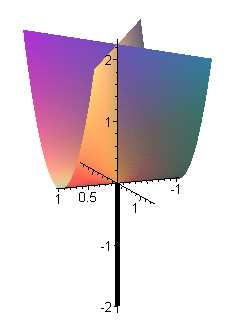
Whitney's umbrella is projectively (and really) equivalent to Plücker's conoid represented opposite (the transformation  maps it onto , which brings the pinch point at infinite back at finite distance).

 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017