Cartesian general equation of a conoid with axis Oz and directrix plane z = mx: f(x, y, z – mx) = 0  with f homogeneous with respect to (x, y), the conoid being right for m = 0. Solving for z yields  with g homogeneous with respect to (x,y), which gives the Cylindrical equation: . Cartesian parametrization:  (). Striction line:  with  (line equal to the axis for a right conoid). First quadratic form in the right case: . Cartesian equation of the conoid with axis Oz, directrix plane z = mx and directrix the curve (C) with equation f(y, z) = 0 in the plane x = a:  If (C) is an algebraic curve of degree n, then the conoid is algebraic of degree between n and 2n. Cartesian parametrization of the conoid with axis Oz, directrix plane z = mx and directrix the curve:  in the plane x = a: . Simple cartesian parametrization of the right conoid with axis Oy and directrix the curve :  in the plane x = a : .

Examples of algebraic conoids:
degree 2: the hyperbolic paraboloid, which is a conoid in two ways
degree 3: all the ruled cubic surfaces, including Plücker's conoid, Zindler's conoid and the parabolic conoids.
degree 4: the cunocuneus.

Examples of transcendental conoids:
    - the right helicoid.
    - the sinusoidal conoid, or Gaudi surface.

Some visual examples:
 

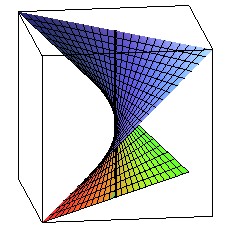
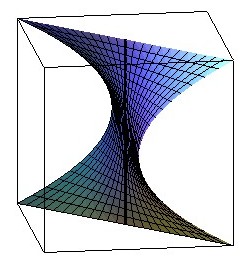
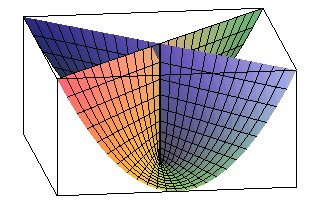
Right conoid with directrix a line neither parallel, nor perpendicular to the axis: hyperbolic paraboloid equation: z =  y /x.	Right conoid with directrix a parabola with axis perpendicular to that of the conoid: see parabolic conoid. equation: z² = y/x	Right conoid with directrix a parabola with axis parallel to that of the conoid: Whitney's umbrella equation: z = (y/x)²

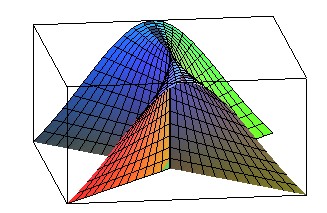
Right conoid with directrix a witch of Agnesi: Plücker's conoid. equation: z = (1 - (y/x)²)/(1 + (y/x)²).	Right conoid with directrix a circle in a plane parallel to the axis: cunocuneus. equation: z² + (y/x)^2 = 1

 

The notion of directrix can be generalized to a surface: the conoid is then defined as the reunion of the lines passing by the axis, parallel to the directrix plane, and with tangents on the directrix surface. For example, here is the case where the directrix surface is the sphere with radius b centered on (a, 0, 0), the directrix plane is xOy, and the axis is Oz: Cartesian equation: (compare to the cunocuneus: ). Cylindrical equation: . Cartesian parametrization:. Parametrization of the tangency curve between the surface and the sphere:. When b = a we get Plücker's conoid of order 1.

 

Any plane curve is the projection of the intersection of a conoid and a cone of revolution; more precisely, the curve with polar equation  in xOy is the projection on xOy of the intersection between the conoid  and the cone of revolution . Opposite, for example, the cardioid  is the projection of the intersection between Plücker's conoid  and the cone of revolution .

Sometimes the term conoidal surface refers to a ruled surface with two linear directrices: the conoid is then the case where one of these directrices is at infinity.
The image of a conoidal surface (and therefore of a conoid) by a homography is a conoidal surface.
The milk carton is an example of such a surface.
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017