,
reunion of the lines Du
passing through 
and directed by 
with 
.
Reduced Cartesian equation of Catalan surfaces with directrix plane xOy with only one line in each plane parallel to xOy:
(reunion of the lines 
),
giving a conoid for 
.| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CATALAN SURFACE
| Surface studied by Catalan
in 1855.
Eugene Charles Catalan (1814-1894): Franco-Belgian mathematician. Other name: ruled surface with directrix plane. |
| Cartesian parametrization: ,
reunion of the lines Du
passing through
and directed by
with .
Reduced Cartesian equation of Catalan surfaces with directrix plane xOy with only one line in each plane parallel to xOy:
(reunion of the lines ),
giving a conoid for . |
A Catalan surface is a ruled surface the generatrices of which remain parallel to a fixed plane, called the directrix plane, in other words, a ruled surface the directrix cone of which is planar.
Examples: the cylinders, the conoids, the ruled helicoids with directrix plane.
The family of lines based on two given curves and parallel
to a given plane generates a surface of Catalan. Taking by
example xOy as plane, we get:
Cartesian parametrization :  ,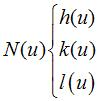
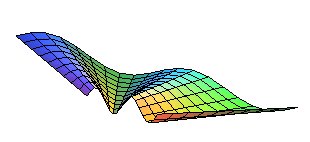
meeting of lines going through 
and  . |
Example of a Catalan surface based on two sinusoids. |
Do not mistake these for Catalan's
minimal surface.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2019