ZINDLER'S CONOID
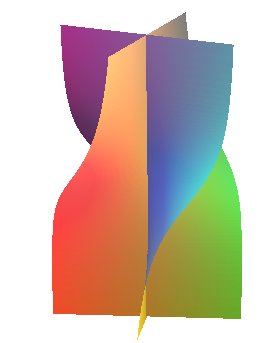
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ZINDLER'S CONOID
| Konrad Zindler (1866 -1934): Austrian mathematician. |
| Cylindrical equation: Cartesian parametrization: Cartesian equation: Rational ruled cubic surface with double line Oz. |
Zindler's conoid is the right conoid
with directrix a cylindrical
tangent wave with 4 branches (here, the wave )
and axis the axis of this wave.
Zindler's conoid is also the right conoid with directrix
a cubic of the type  located in a plane parallel to its axis.
located in a plane parallel to its axis.
Any cylinder with generatrix Oz and directrix a rectangular hyperbola perpendicular to the axis cuts Zindler's conoid at hyperbola (in red) plus the axis Oz (in blue).
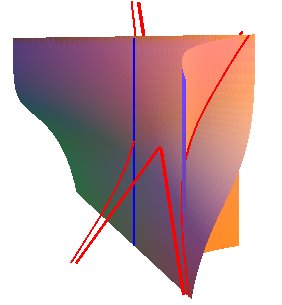
The complex scaling
transforms it into Plücker's conoid,
but these two conoids are images of one another by a real homography.
this can be generalized to any cylindrical tangent wave,
which gives the cylindrical equation:
;
| The case n = 1 gives the rectangular hyperbolic
paraboloid |
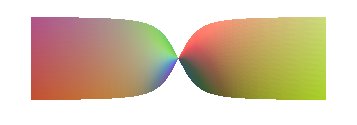 |

Case n = 3
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL L.G. VIDIANI 2017