Ruled cubic

RULED CUBIC (SURFACE)

The ruled cubics are the ruled ,algebraic surfaces of degree 3.

See here a proof of the following statements.

Apart from the cones and the cylinders with directrix a plane cubic, the other ruled cubics, so-called skew ruled cubics, can all be defined in the following way:

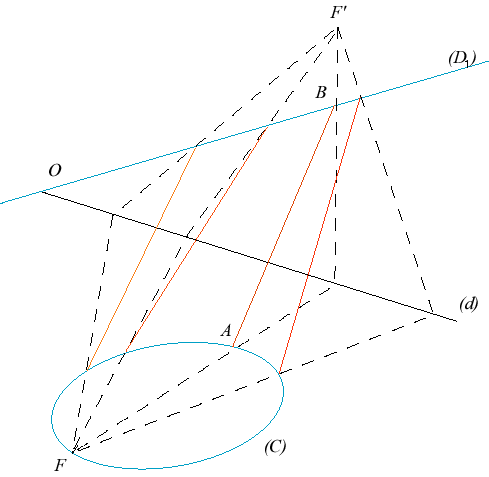
Given a conic (C) located in a plane (P), a line (D₁), cutting (P) at O, a homography between the points A of (C) and B of (D₁) such that O is not a double point, the ruled cubic is the union of the lines (AB).

Figure showing the construction of a homography between the conic (C) and the line (D₁), thanks to a line (d) of the plane of the conic.

Then, there are two complex projective equivalence classes depending on whether the line (D₁) and the conic (C) intersect at O (special case of the so-called "Cayley ruled surfaces", not to be mistaken for "the" Cayley surface) or not.

In the non-intersecting case, the surface has another directrix (D₂) that meets the conic (C) so the surface, which thus has two linear directrices (D₁) and (D₂), is a conoidal surface, and can be defined as the union of the lines meeting (D₁), (D₂) and (C); the line (D₂) is the double line of the surface and contains two pinch points K and K' of the surface corresponding to the points where the generatrix and the directrix (D₁) form a plane tangent to the conic (C).
These two pinch points are real or imaginary depending on whether through O there pass, or not, real tangents to the conic (C), and these two case constitute two different real projective equivalence classes.
In the first one (real pinch points) we can find Plücker's conoid and Whitney's umbrella, and in the second one (imaginary pinch points) we can find Zindler's conoid and the Möbius surface.

Remark: when O is a double point of the above homography, the surface defined degenerates into a quadric.

The skew ruled cubics are all rational, and are special cases of Steiner surfaces.

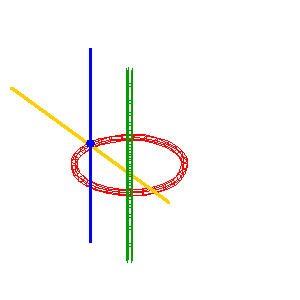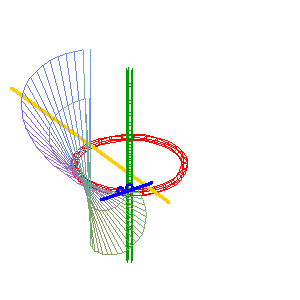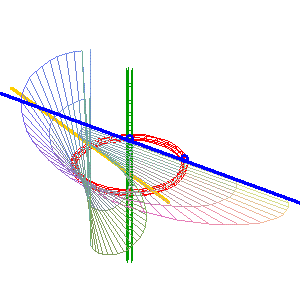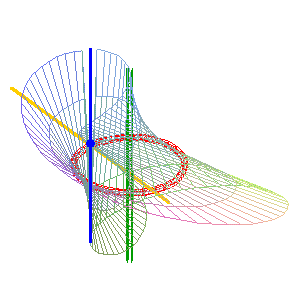
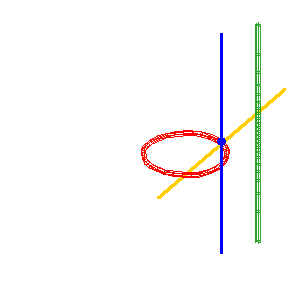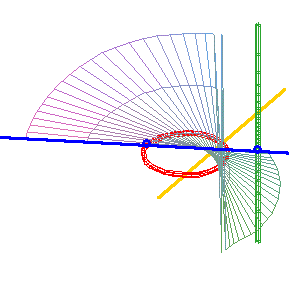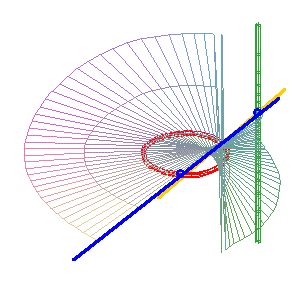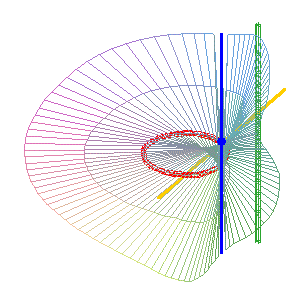
A common case with real pinch points
(b = 0): the simple line (D₁) (green) is inside the circle, the other line is the double line (D₂) .
Here, the surface obtained is the Möbius surface.

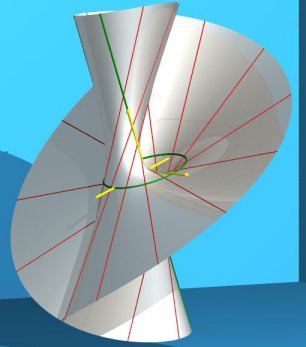
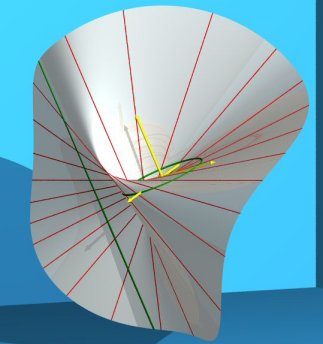
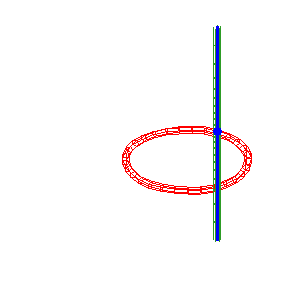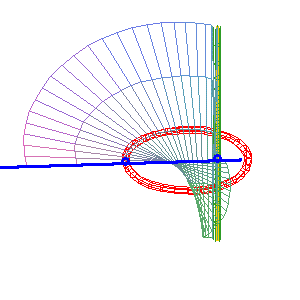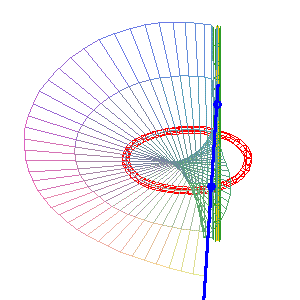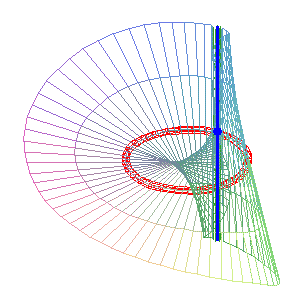A common case with two real pinch points (b = -2a): the simple line (green) is outside the circle.

Special case (b = -a):
Cayley ruled surface
the simple line (D₁) (green) is secant to the circle and equal to (D₂).

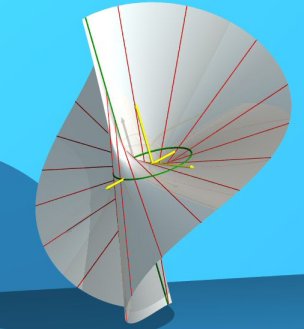For the animations above, we chose
as conic (C) the circle , with current point
and as simple line (D₁) the line , with current point (the transform is indeed a homography).
The double line (D₂) is then , with current point .

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra