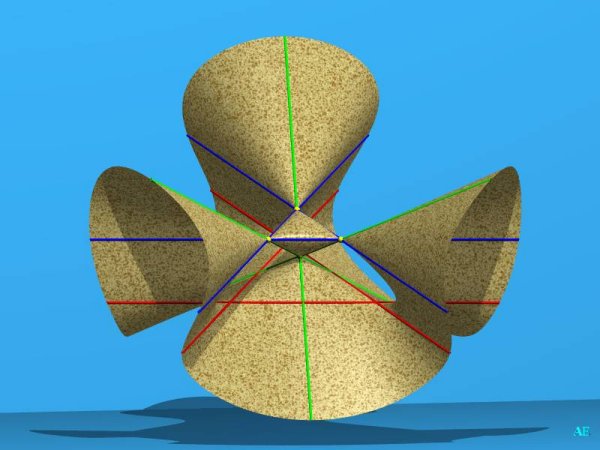
Second form

Third form

Form #1 Homogeneous equation said to be tetrahedral: , i.e. . Cubic surface. The 4 conical points are . The 9 lines are the 6  for   (the line  joins  and ) and the 3  for . In the associated affine version, with equation , there remains only one conical point at finite distance A4 and 3 included lines (the 3 axes, in black opposite).

The Cayley surface is the surface defined (up to homography) by the above equation.

It is the only cubic surface for which the homography group under the action of which it is invariant is the group S₄ of permutations of 4 objects (cf. the invariance under the 24 permutations of the coordinates ) and it is also the only cubic surface to have 4 conical points (maximum possible for a cubic surface).
This non smooth surface has 9 lines, which are real: the edges of the tetrahedron formed by the conical points and 3 other lines, which are coplanar.

A first projective transform enables us to "see" the 9 lines at finite distance:

Form #2 The change of coordinates defined by  gives the  Homogeneous equation 2: . The conical points are . The 9 lines are the 6 edges of the tetrahedron formed by the conical points, plus: , , . Associated affine Cartesian equation: . The conical points are  The 9 lines are the 6 edges of the tetrahedron formed by the conical points, plus: ,, .

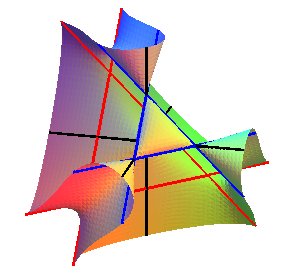The axes of the frame are in black, the three other edges of the tetrahedron in blue, and the three lines  in red. We chose here k = 2 (for k = 1 the lines  are at infinity). In this case, it can be proved that the Cayley surface is the locus of the points the projections of which on the four plane-face of the tetrahedron formed by the conical points are coplanar. It is, in some way, the generalization to space of the problem of the locus of the points for which the projections of the sides of a triangle are aligned, such locus being the circumscribed circle of the triangle (cf Simson line).

A second projective transform gives an affine view in which the surface is invariant under the 24 isometries of the regular tetrahedron (but 3 of the 9 lines are at infinity):

Form #3 The change of coordinates defined by  gives the  Homogeneous equation 3:  ; The conical points are . The 9 lines are the 6 edges of the tetrahedron and . Associated affine Cartesian equation:  (see sine surface for a simpler parametrization) The conical points are  ,  forming a regular tetrahedron the 6 edges of which are the lines  (the lines  are at infinity in this model). The rotation of an eighth of a turn defined by  gives the Cartesian equation: , which simplifies to  The volume of the tetrahedral part is equal to . Under this form, the Cayley surface is a tetrahedral surface of Goursat.

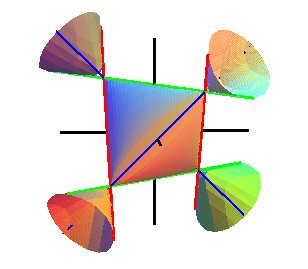View with the 3 coordinate axes (in black) and the 6 included lines.

The third projective transform below gives the so-called "pentahedral" form, that all cubic surfaces have (Sylvester-Clebsch theorem):
 

Form #4 The change of coordinates defined by  gives the  Homogeneous equation 4:  ; The conical points are . The nine included lines are the 6 edges of the tetrahedron and , , . Associated affine Cartesian equation: . The conical points are . With , we get the so-called "pentahedral" homogeneous equation in :  (compare to the pentahedral equation of the Clebsch surface).

View with the 6 edges of the tetrahedron (in blue, yellow, and green) and the three lines  in red. Link to an applet allowing to manipulate the figure formed by the lines included in the surface.

Do not mistake for the ruled Cayley surfaces.

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL Alain ESCULIER 2017