Surface considered and named by Gray in 1997, but studied before?

 

Cartesian parametrization:. Cartesian equation:  where, or also. Sextic surface.

 

The sine surface is a union of ellipses, like the animation opposite shows, and this in 3 different ways (sections by the planes parallel to the coordinate planes). It is a surface with the symmetries of the cube, hence that can be seen as a generalized Goursat surface.

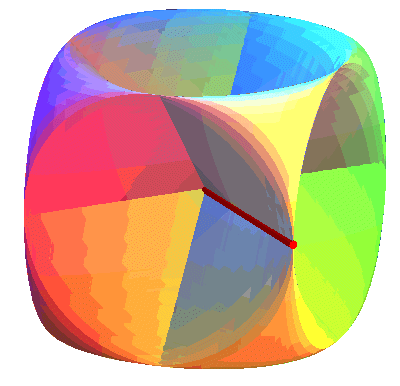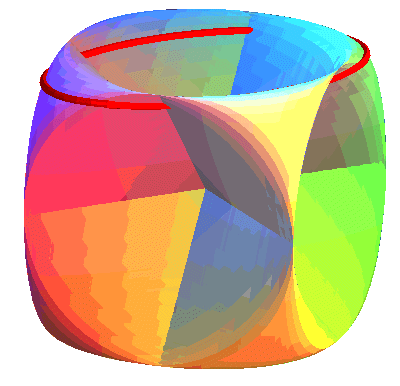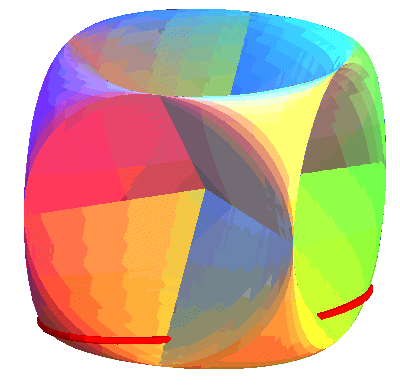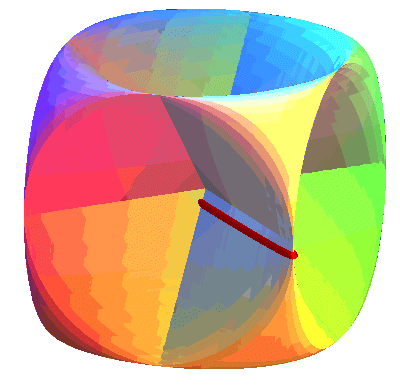Disregarding the 3 segment lines of self-intersection, the sine surface is homeomorphic to the torus (it therefore provides an immersion of it). But, as opposed to the classic geometric torus for which the inside face is hidden, the two faces of this orientable surface have as many visible and invisible parts; and a rotation of  around Oz constitutes a twist of the torus. Note that if the surface is oriented, then it only has the symmetries of the tetrahedron; for example, a symmetry with respect to xOy changes the orientation.

The two faces of the sine surface.

View of the two surfaces  that constitute the complete surface.

 

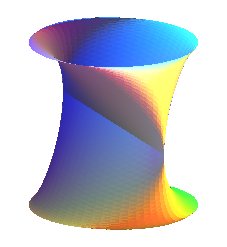View of the 4 surfaces (for the 4 permutations of the signs) that constitute the complete surface. Each of them touches the 3 others.

 

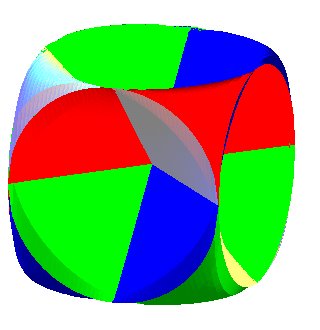A polyhedral version of the sine surface is the octahemioctahedron, which has the same segment lines of self-intersection.

 

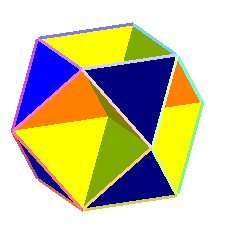The surface which, by symmetry, could be called the cosine surface:  is none other than the tetrahedral part of the Cayley surface: .

 

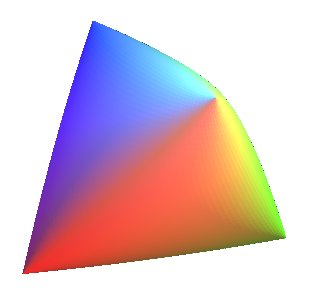Sine surface engraved by Patrice Jeener

 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017