Family of surfaces studied by Goursat in 1887. Edouard Goursat (1858 - 1936): French mathematician.

 

Cartesian equation: . Quartic surface.

The (octahedral - best to avoid "cubic") Goursat surfaces are the quartic surfaces that have the symmetries of the cube (or, which amounts to the same thing, the octahedron).
More precisely, they are the quartics such that the isometry group under the action of which they are invariant is the same as that of the cube.
The general form in Cartesian coordinates is given above.

Some remarkable special cases:
 

View obtained with Maple	(k, k', k")	Equation, comment	Povray view, by Alain Esculier
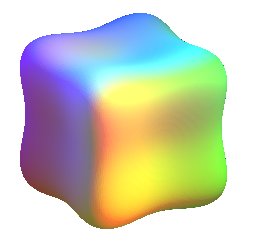	(0, –1, 0)	Rounded cube passing by the vertices , and the middles of the edges , and the centers of the faces  of the cube: .
	(–1,–1/4,1/4)	Rounded octahedron passing by the vertices  and the middles of the edges  of the octahedron: .
	(–1, 1, 1)
	(0, –2, 2)	Surface with 12 singularities  at the vertices of a cuboctahedron.
	(–1/2, -1, 1/2)	Surface containing the 12 extended edges of the octahedron: , for example . It is to the octahedron what the Cayley surface is to the tetrahedron.
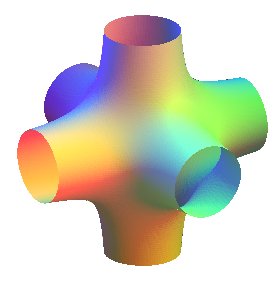
	(–1/2, 1, -3/2)	Surface containing the 12 diagonals of the faces of the cube , for example x = y , z= a. It is to the cube what the previous surface was to the octahedron.
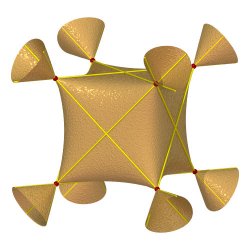	(–1, 4, –6)	. Surface containing the 12 extended edges of the cube , for example x = y = a.
		Same surface as before!
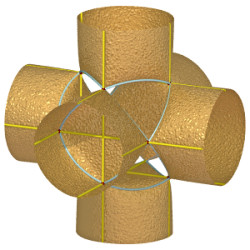
	(–1, 2, –2)	Surface with 12 singularities  at the vertices of a cuboctahedron and containing the 12 extended medians of the faces of a cube, for example, z = 0, x = a. It is composed of 6 sheets with bases the square faces of the cuboctahedron.
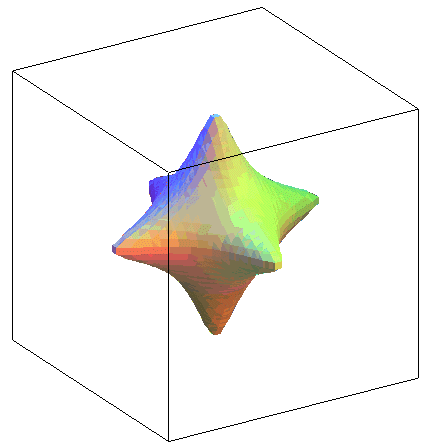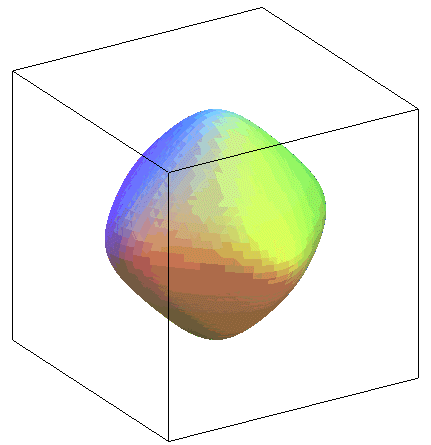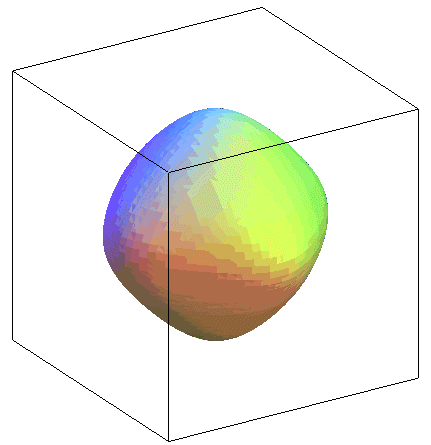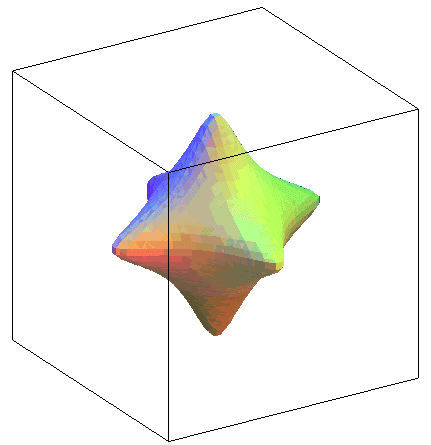
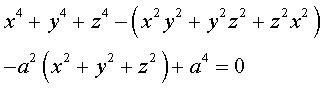
	(-1/3,-2/3,2/3)	Surface with 12 singularities  at the vertices of a cuboctahedron. It is composed of 8 sheets with bases the triangular faces of the cuboctahedron.

 

Animation of the case  and an example with k" = 0.02.

More generally, the Goursat surfaces are the algebraic surfaces with the symmetries of a regular polyhedron, the simplest after the sphere.

The general equation of the tetrahedral Goursat surfaces, of degree 3, is: .
For k' = 0, we get the Titeica surface;, and in the other cases, up to changing a into a/k', we can assume k' = 1, and we get the family with one parameter  that behaves as follows:
 

k < 0, k = 0 Four sheets, plus, in the case k = 0, the isolated point O.	0 < k < 4 A rounded tetrahedron plus 4 sheets.	k = 4 Cayley surface	k > 4

Views of the quartic with equation  that has the symmetries of the tetrahedron (notice the 4 "triconical" points,  with an odd number of minus signs).

The general equation of the dodecahedral Goursat surfaces, of degree 6, is:

Some remarkable special cases:
 

	(k, k',k",k''')	Equation, comment
	(0, 0, 0, 0)	i.e. Surface that decomposes into the 6 planes passing by the edges of an icosidodecahedron (the plane z = 0, the plane z = 2x and its 4 images by rotations of  radians around Oz).
	(1,–1,1,–1)	Rounded dodecahedron.
	(–1,0,–1,1)	Rounded icosahedron
	(0,1,–2,1)	Surface with 30 singularities at the vertices of an icosidodecahedron. It is composed of 20 sheets with bases the triangular faces of the icosidodecahedron.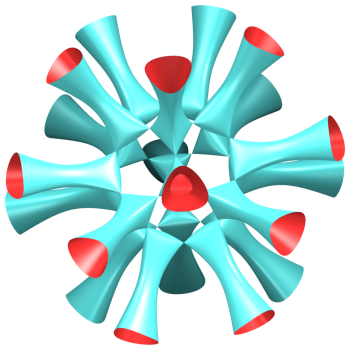
	(0,–1,2,–1)	Surface with 30 singularities at the vertices of an icosidodecahedron. It is composed of 12 sheets with bases the pentagonal faces of the icosidodecahedron.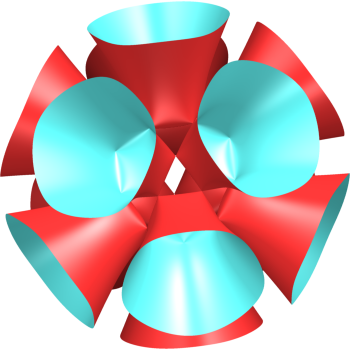
	(0,5/4,–5/2,5/4)	Barth sextic, with fifty singularities.

 

We can impose on the surface of equation given above to contain a line not passing by O, and we then note that the surface has exactly 60 lines, images of one of them by the 60 rotations of the group of isometries of the dodecahedron.  For example, the value of (k, k ', k ", k''') for the surface to contain the line x = -2z, y = a is (-1, 8, -18, 11); in this case, the lines are grouped in 6 groups of 10 parallel lines forming six cylinders whose axes are those which join the opposite vertices of a regular icosahedron.

See other superb Goursat sextics in relief on this page of Alain Esculier.

See also the Goursat curves, the surfaces invariant under the action of a half-turn, the surfaces with rotational symmetry.

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017