Hanging drop of water

HANGING DROP OF WATER

Homemade name.

The hanging drop of water is the surface of revolution the curvature of which is, at any point, proportional to the distance to a plane perpendicular to its axis; according to Laplace's theorem, it models the shape of a drop of water hanging at the end of a vertical circular pipe.

For a surface of revolution obtained by the rotation around Oy of the curve x = f(t), y = g(t), the zero curvature plane being the plane perpendicular to Oy passing by O, the differential relation: can be w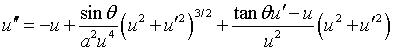ritten, since:
with: or
or (the derivatives are taken with respect to theta).

The profile of the cylindrical surface the curvature of which is proportional to the distance to a plane perpendicular to its axis is a lintearia.

We can also consider the surface of revolution the curvature of which is, at any point, proportional to the distance to a plane containing its axis:

The differential relation: can be written:
or: which integrates to i.e. .

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra