WILMORE'S TORUS
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
WILMORE'S TORUS
| Links:
Wikipedia article on the Willmore conjecture www.chem.ucla.edu/~michalet/papers/larecherche/f-tores.html torus.math.uiuc.edu/jms/Images/will.html |
Willmore's torus is the torus
for which the ratio of the major and minor axes is equal to 
.
The energy of curvature of a surface S,
or total mean curvature, beeing defined by the integral 
where 
is the mean curvature, the Willmore's torus is the torus with minimal energy.
Thus, for a torus of major axe
a and minor axe b, the energy
E
is 
, that
is minimal when 
,
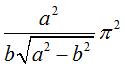
with the value 
.
Willmore conjectured in 1965 that
is the minimal value of the energy of all orientable surface of genus
1 (conjecture proved in 2014). The surfaces of genus 1 reaching this minimum
value are Willmore's torus and its inverses (thus particular Dupin
cyclids).
This was verified through experimentation by the shapes assumed by liposomes.
Note that the total absolute Gaussian curvature,
defined by 
where 
is 
for
each torus. Sea also the tight surfaces.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2019