| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
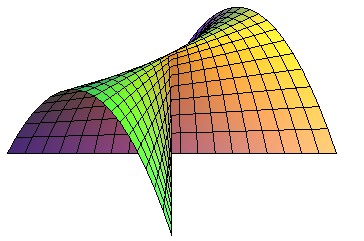
PARABOLIC CONOID
A parabolic conoid is a conoid a directrix of which is a parabola; it is therefore the reunion of the lines supported by a line (D), a parabola (C) and parallel to a plane (P).
When the conoid is right ((D) and (P) perpendicular) and the axis of the parabola is parallel to (D), we get Whitney's umbrella.

| Cartesian equation : Ruled cubic surface. |
Cas a=b |
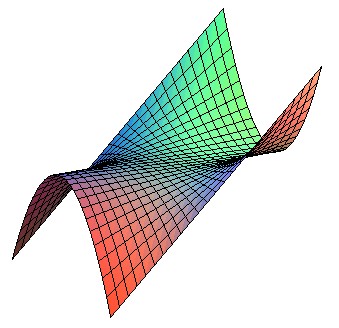 |
This surface is projectively (and really) equivalent to Whitney's umbrella, and therefore to Plücker's conoid .
When the parabola and the axis of the conoid intersect, the surface is a hyperbolic paraboloid.
Picture from this
website.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2020