Bernard Morin (1933-2018) : mathématicien français. Article de B. Morin et J.P. Petit sur le retournement de la sphère : new.lutecium.org/www.jp-petit.com/science/maths_f/Retournement_sphere/PLS_79.pdf François Apéry : models of the projective plane, page 104. en.wikipedia.org/wiki/Morin_surface mathinfo.unistra.fr/fileadmin/upload/IREM/Publications/L_Ouvert/n094/o_94_32-45.pdf http://www.math-art.eu/Documents/pdfs/Cagliari2013/Cagliari_Denner_Springer-009.pdf

 

Paramétrisation cartésienne de François Apéry :  où

 
 

La surface de Morin est une immersion de la sphère intervenant dans la phase centrale du retournement de la sphère imaginée par B. Morin et J.P. Petit (cf. article ci-dessus). Le dessin de J.P. Petit ci-contre en montre la topologie. La sphère avait au départ une face colorée en gris et une face colorée en orange. L'échange des deux faces se fait dans la phase centrale du retournement par une simple rotation de .
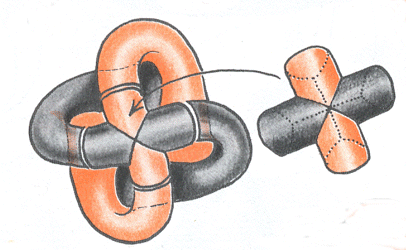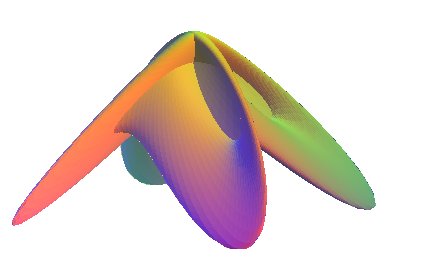
Pour n = 2 et k = 1, la paramétrisation ci-dessus en donne un modèle (le cas  n = 3, k = 1 donne la surface de Boy).
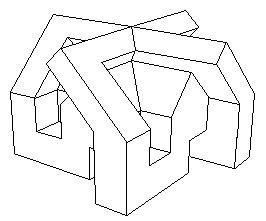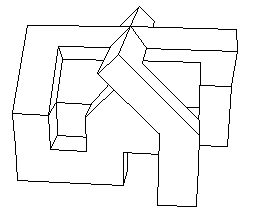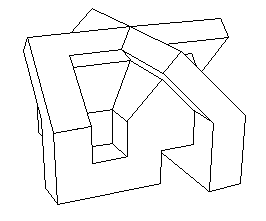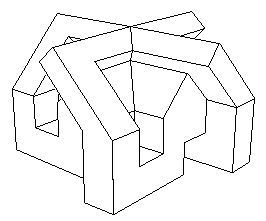
Ci-contre, une version polyédrique de cette surface dûe à J.P. Petit. Une autre version est dûe à Richard Denner (voir les liens ci-dessus).
La paramétrisation d'Apéry fournit une famille de surfaces à symétrie de rotation d'ordre n ; ci-contre le cas n = 5.

 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017