Notion étudiée par Euler et par Auguste Miquel en 1838 (Journal de mathématiques pures et appliquées p. 202 à 208). Autres noms : donné par Miquel : courbes syntrépentes, littéralement "qui tournent ensemble", courbes roulantes. Voir aussi le blog de Manuel LUQUE.

Deux courbes  et  sont appelées profils conjugués associés aux centres de rotation O₁ et O₂ (les moyeux des engrenages) si on peut faire tourner  autour de O₁ et  autour de O₂ de sorte que les deux courbes restent constamment en contact (c'est-à dire tangentes sans glisser l'une sur l'autre).

Pour obtenir la courbe  connaissant la courbe , le moyeu  O₁ et la distance d = O₁O₂ , il suffit de déterminer le mouvement plan sur plan dont la base est  et une roulette est le cercle de centre O₁  et de rayon d : la roulante est alors la courbe .
 

En désignant par les coordonnées polaires du point courant de  dans un repère centré en O1, et de même  pour  dans un repère centré en O2, les relations entre  et  sont données par :   Dans le cas d'un roulement des deux courbes en sens contraire : Si donc l'équation polaire de  est mise sous la forme, l'équation polaire de  est  où g est définie par :  . Autrement dit une paramétrisation polaire de   est . Si l'équation polaire de  est mise sous la forme , l'équation polaire de  est  . Dans le cas d'un roulement des deux courbes dans le même sens : Si donc l'équation polaire de  est mise sous la forme , l'équation polaire de  est  où g est définie par :  . Autrement dit une paramétrisation polaire de   est . Si l'équation polaire de  est mise sous la forme , l'équation polaire de  est  . Remarque : cette distinction n'est pertinente que si l'on considère  et  positifs. Si l'on accepte des valeurs négatives, le cas 2 équivaut au cas 1 en changeant  en son opposé.

Remarque : d'après le théorème de Descartes, le point de contact entre les deux profils conjugués est constamment aligné avec les deux moyeux.

Exemples :
    - si  est un cercle de rayon a et le moyeu en son centre,  est un cercle de rayon |d - a|.
    - si  est rectiligne, situé à une distance a de O,  a pour équation , ce qui donne :
 

si d > a :  avec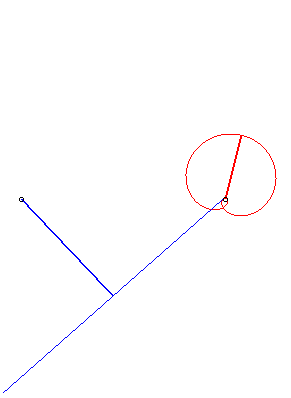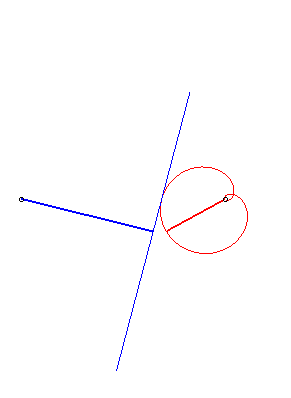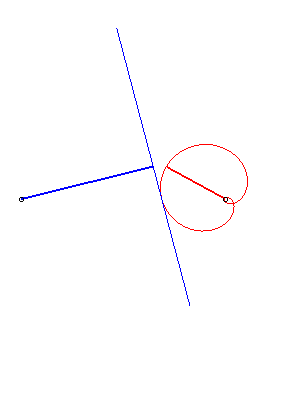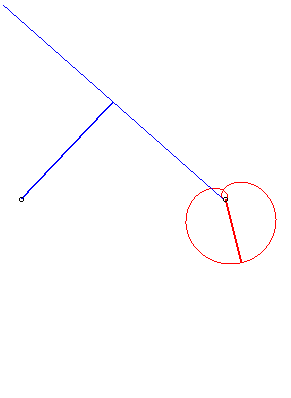

si d = a :

si d < a :  avec  (polygastéroïde avec e > 1)

    - si  est une ellipse, d'équation polaire  (le moyeu est donc en un foyer),  est une polygastéroïde, d'équation polaire , avec  (n représente le nombre de tours effectués par  pour que  fasse un tour) ; si  est le demi-grand-axe de l'ellipse, les distances des moyeux sont données par  pour des engrenages tournant en sens contraires, et  pour des engrenages tournant dans le même sens.
 

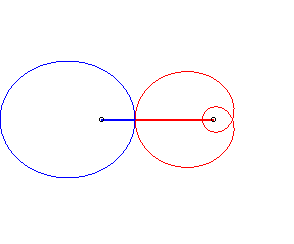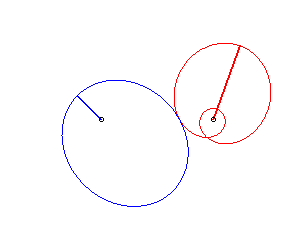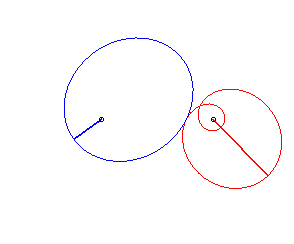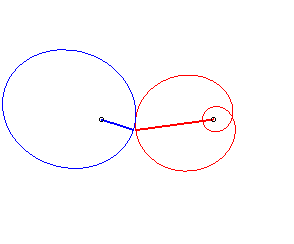
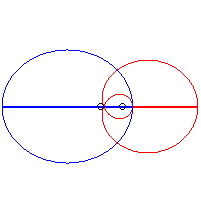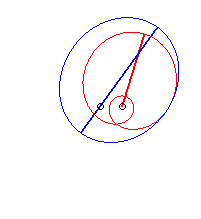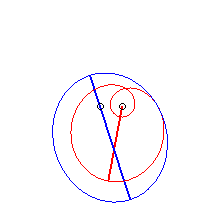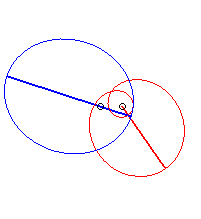
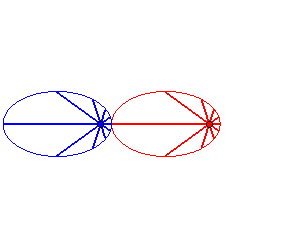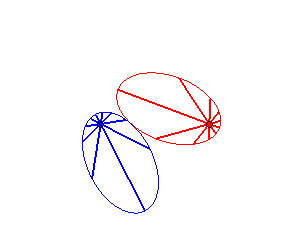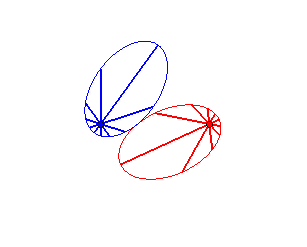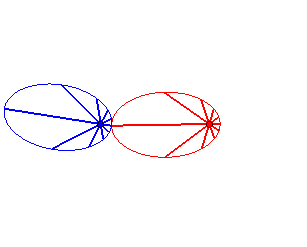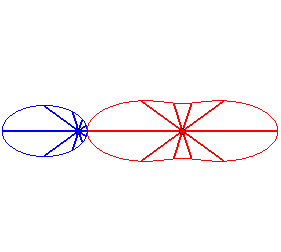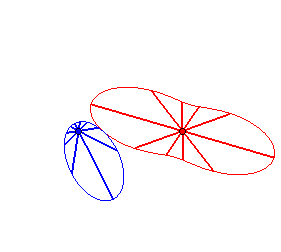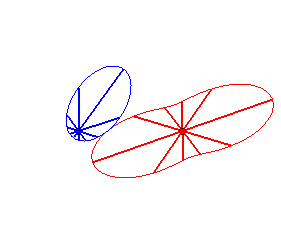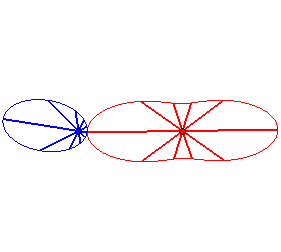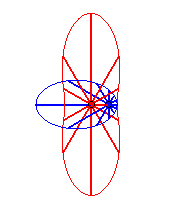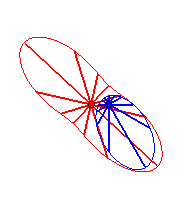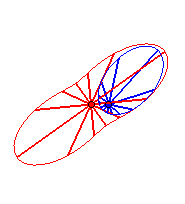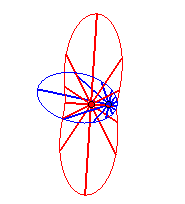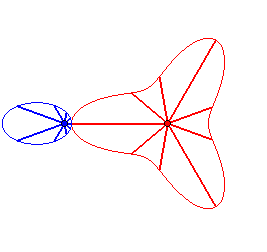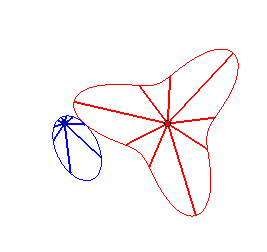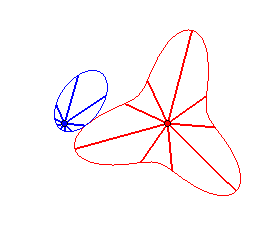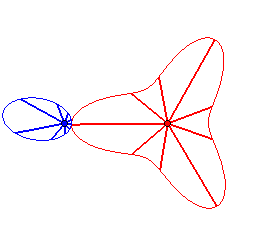
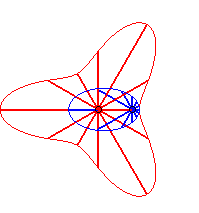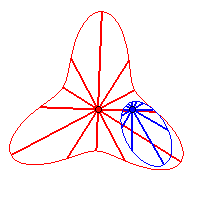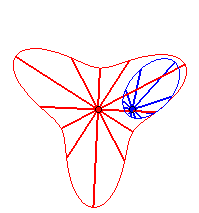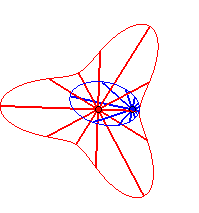Cas n = 1 (soit k = 2) :  est une ellipse isométrique à  ; on dit que l'ellipse est isotrépente pour son foyer.	Cas n = 2 :  est une inverse de cacahuète. Remarque : pour une excentricité plus faible (inférieure à )  l'ellipse est incluse dans sa conjuguée.
Cas n = 3 :	Cas n = 1/2

REM : si  est une hyperbole, on a la même propriété, non illustrée ici, car l'hyperbole est une courbe non fermée. Voir le cas n = 1 sur la page de l'hyperbole.
 

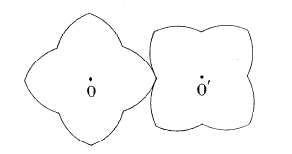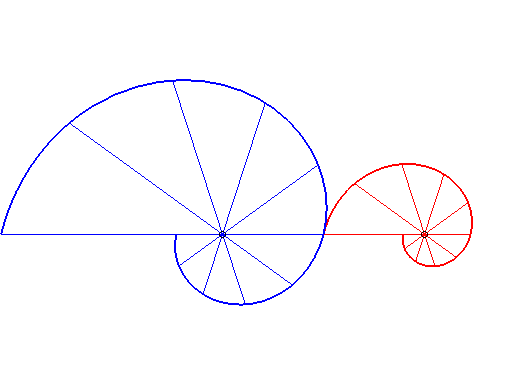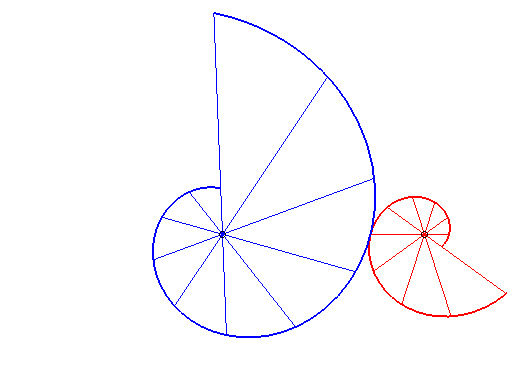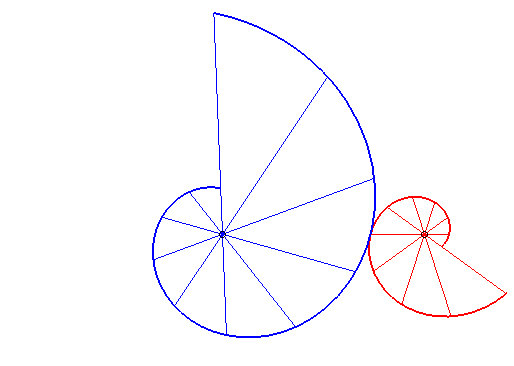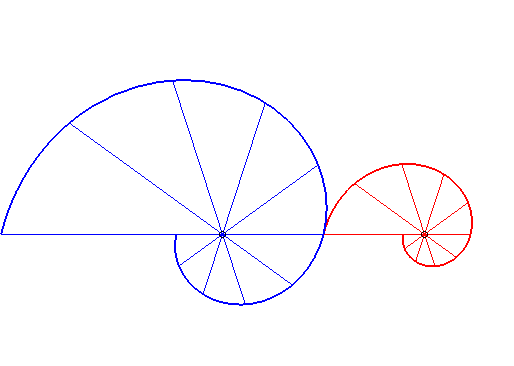- si  est une spirale logarithmique,  est une spirale logarithmique isométrique ; la spirale logarithmique est donc aussi une courbe isotrépente. Ce mécanisme a été découvert par l'astronome Ole Rømer. Il est utilisé dans le système "varistart", permettant d'augmenter progressivement la vitesse de rotation d'un engrenage. Cames formées d'arcs de spirale logarithmique, dessin de Henri Bouasse.

 
 
 

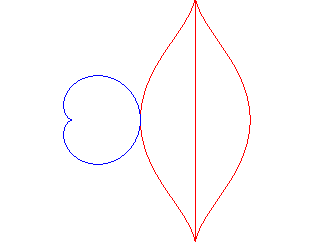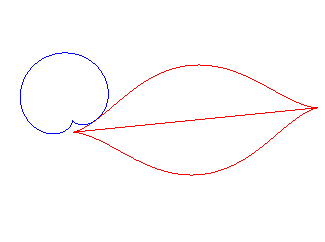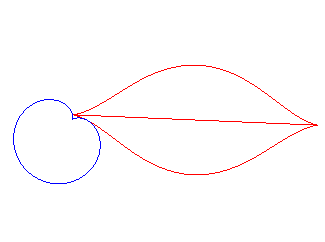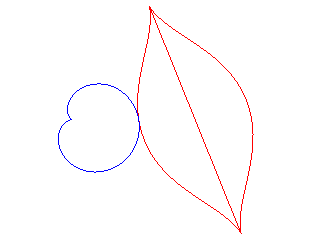
- si  est une cardioïde : (moyeu au point de rebroussement),  a pour paramétrisation :  (d = ka). Ci-contre, le cas k = 18/5.	La bouche au coeur...
si 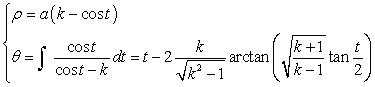 est un cercle :  (moyeu sur le cercle),  a pour paramétrisation :  (d = ka). Ci-contre, le cas k = –5/3.

 

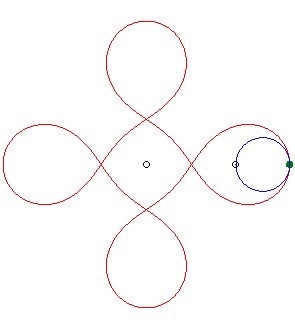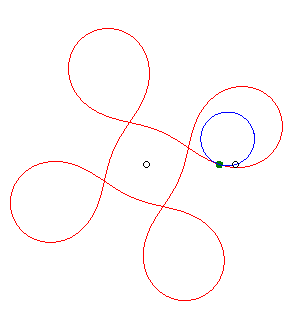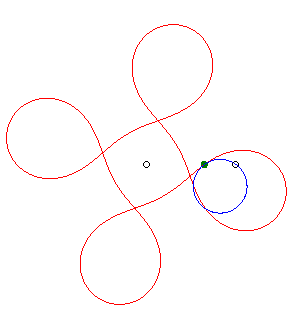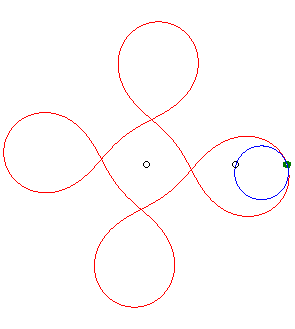Engrenages de Schroeder datant de 1867, provenant du Musée des Arts et Métiers. La courbe inférieure  est un limaçon de Pascal à méplat. Voir aussi ce lien.

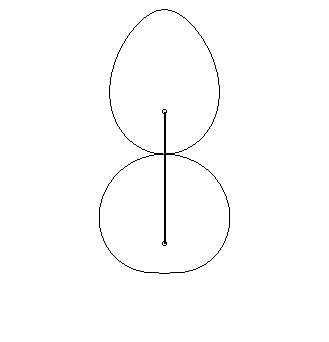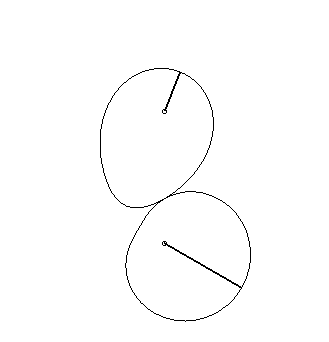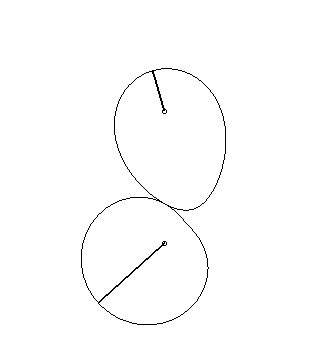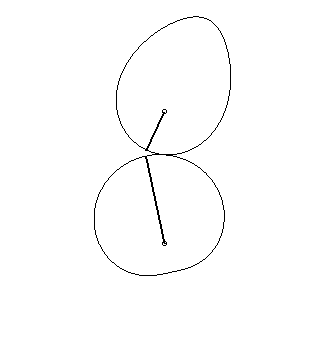Lorsque le moyeu de l'un des engrenages est à l'infini, on obtient un couple roue-route.
 
 

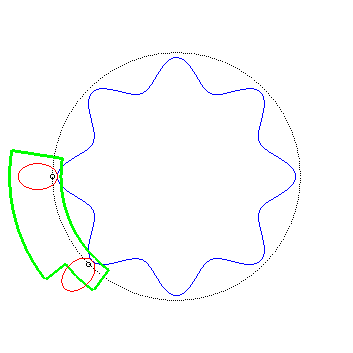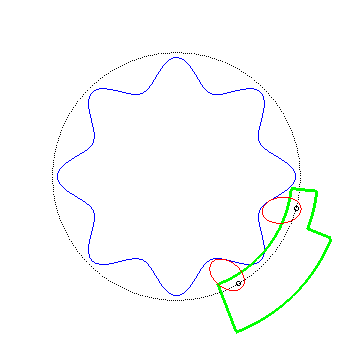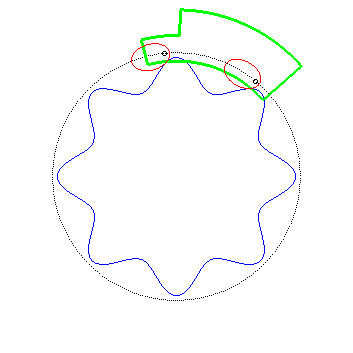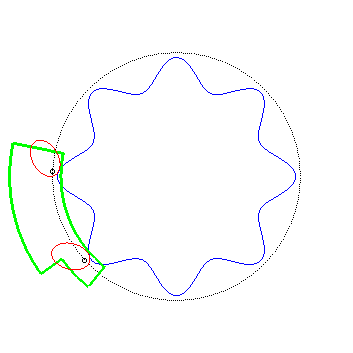
On a vu ci-dessus que si l'on fixe l'un des engrenages et que l'on fait rouler l'autre dessus, le moyeu de ce dernier décrit un cercle ; ceci permet d'envisager des véhicules shadocks comme celui représenté ci-contre ... (réalisation Alain Esculier : voir au bas de cette page) Pour des véhicules similaires, mais à mouvement rectiligne, voir la page suivante.

Voir aussi les engrenages hyperboloïdes, généralisation à l'espace de cette notion plane, en bas de cette page.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Jean LEFORT, Alain ESCULIER  2018