DELTOÏDE
Deltoid
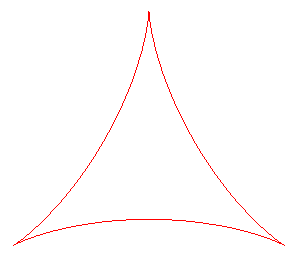
or three-cusped hypocycloid, Deltoide (od. Dreispitzige)
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
DELTOÏDE
Deltoid
or three-cusped hypocycloid, Deltoide (od. Dreispitzige)

| Courbe étudiée par Euler en 1745 et Steiner
en 1856.
Delta : lettre grecque rappelant la forme de la courbe. Autres noms : hypocycloïde à 3 rebroussements, H3, hypocycloïde de Steiner, ou tricuspide. |
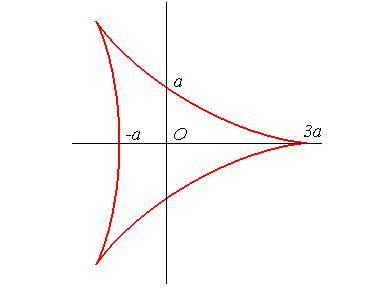 |
Paramétrisation complexe : Paramétrisation cartésienne : Équation cartésienne : Quartique circulaire rationnelle. Paramétrisation polaire : Abscisse curviligne : 1) 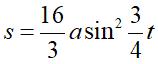 . .
Angle tangentiel cartésien : 1) Rayon podaire : 1) Rayon de courbure 1) Équation intrinsèque 1 (forme 1)) : Équation intrinsèque 2 (forme 1)) : Équation podaire : Longueur : Aire : |
La deltoïde est l'hypocycloïde à trois rebroussements (cercle de rayon a roulant à l'intérieur d'un cercle de rayon 3a).
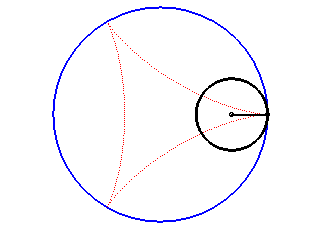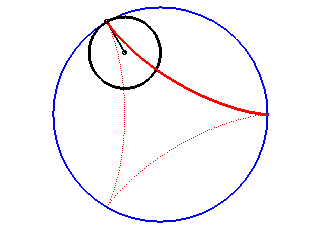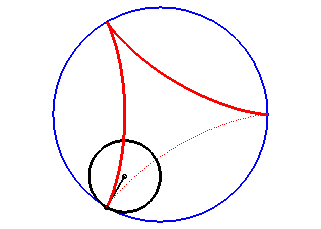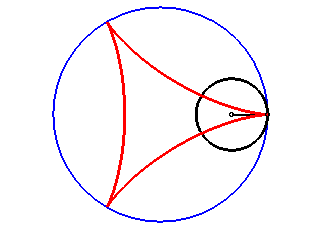
| D’après la double génération des hypocycloïdes, un point d'un cercle de rayon 2a roulant à l'intérieur du cercle de rayon 3a décrit une deltoïde isométrique, mais en sens inverse et l’un de ses diamètres enveloppe aussi une deltoïde isométrique. | 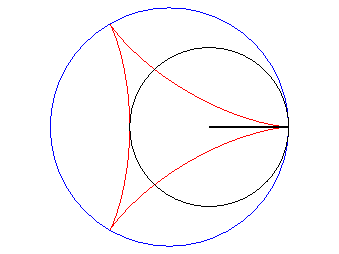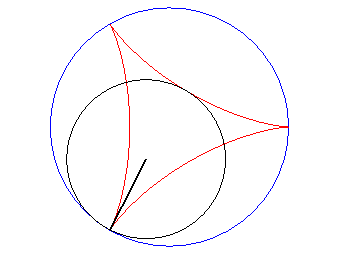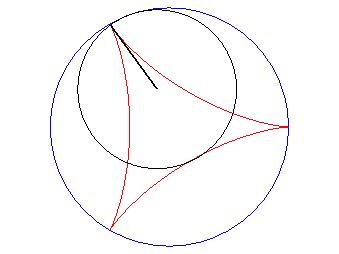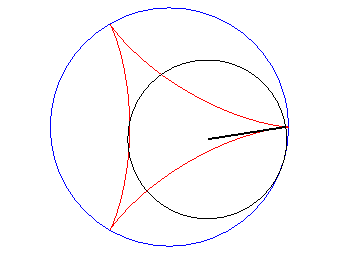 |
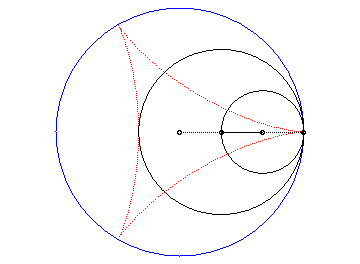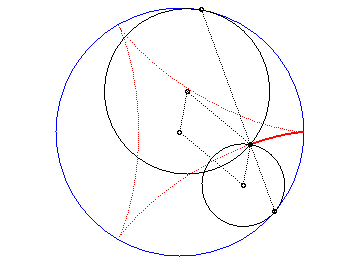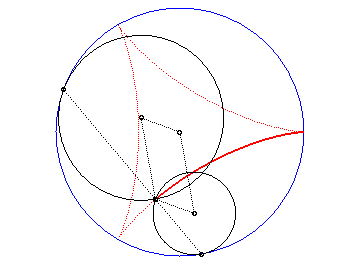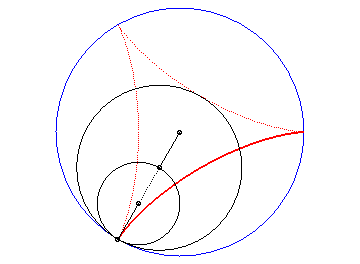
Animation ralentie de la double génération |
| La deltoïde est aussi l'enveloppe d'une corde (PQ) du cercle de centre O et de rayon a (cercle inscrit dans la deltoïde), P et Q parcourant ce cercle dans des sens contraires, l’un ayant une vitesse double de l’autre (génération de Cremona). | 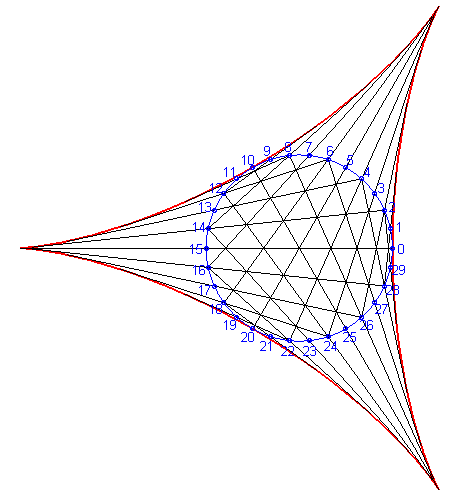
Ci-dessus, le point n est relié au point -2n modulo 30. |
 |
| Mais la plus élégante génération tangentielle est celle décrite ci-contre : les deux points traceurs P et Q décrivent la deltoïde, et la droite (PQ) reste tangente à cette même deltoïde ! |
|
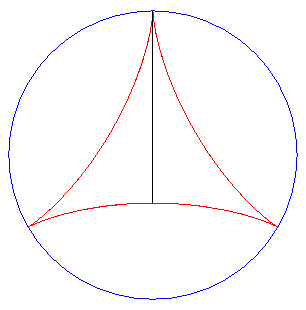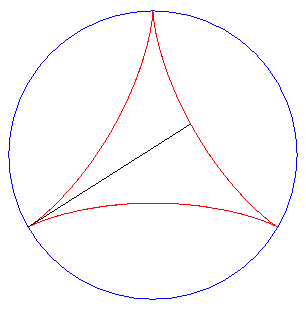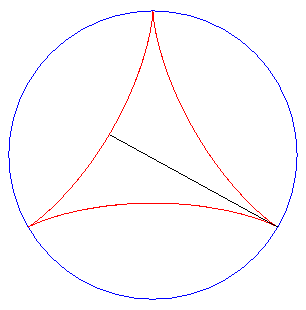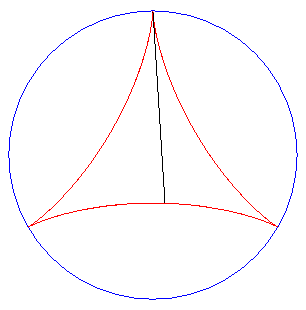
| De plus, le fait que la longueur PQ reste constante
donne une réponse (partielle) au problème
dit de Kakeya : comment retourner une aiguille (de longueur 1) dans
le plan de sorte qu'elle balaie une aire la plus petite possible ?
Ici, l'aire balayée vaut REM : attention : l'aiguille glisse sur la deltoïde lors de son déplacement ! |
 |
| Une autre construction mécanique de la génération tangentielle, duale de la précédente, à partir de l'épicycloïde à 3 rebroussements. |
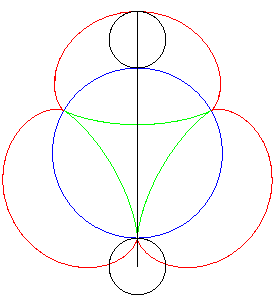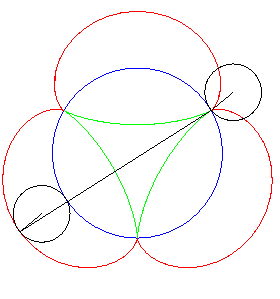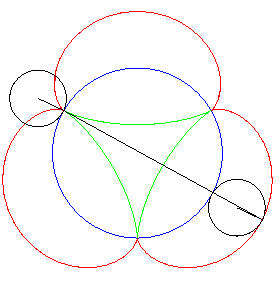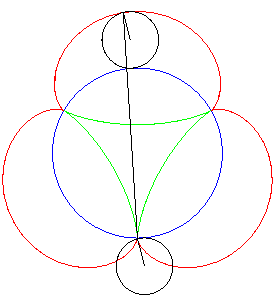 |
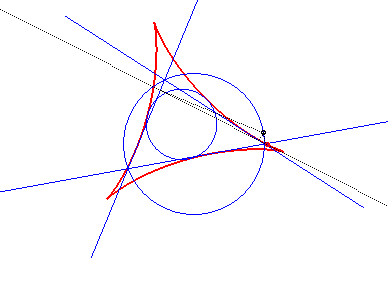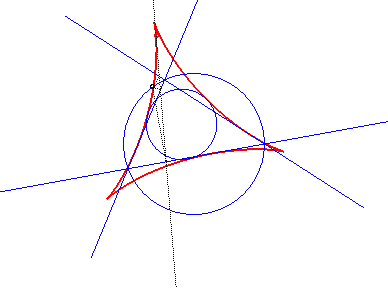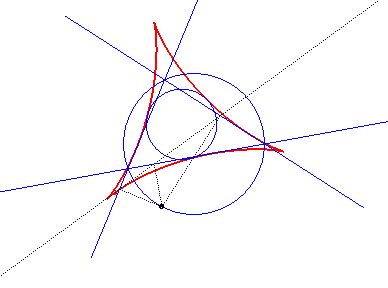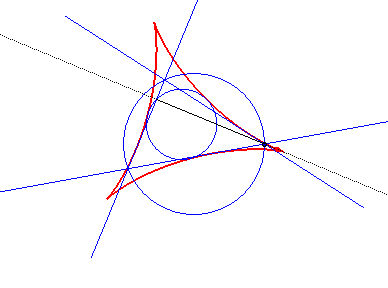
| L'enveloppe des droites
de Simson (qui passent par les projetés sur les trois côtés
d'un point du cercle circonscrit ) d'un triangle quelconque est une deltoïde
centrée au centre du cercle d'Euler du triangle, appelée
hypocycloïde
de Steiner du triangle.
Voir des précisions sur wikipédia. |
 |
|
Comme pour toute courbe cycloïdale, la développée de la deltoïde est une deltoïde semblable (dans un rapport 3) : |
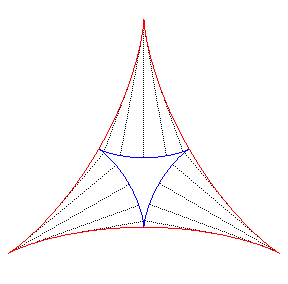 |
|
L'une des développantes est donc une deltoïde ; les autres sont auto-parallèles : |
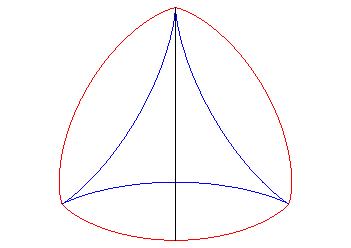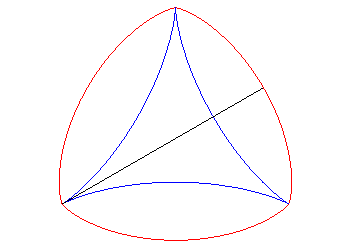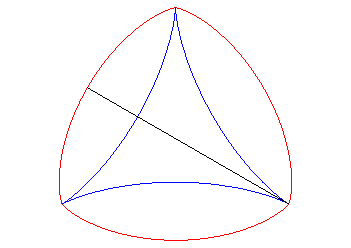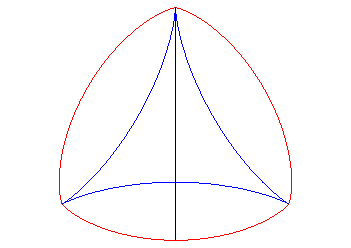 |
Les podaires de
la deltoïde sont les foliums,
et l'antipodaire d'une ellipse par rapport à un sommet principal
donne une deltoïde dilatée (voir à courbe
de Talbot).
Ses caustiques par réflexion
au soleil sont des astroïdes.
Son orthoptique
est son cercle inscrit.
Sa radiale est
un trifolium régulier.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2015