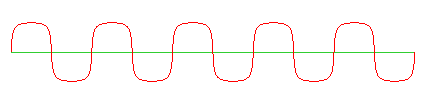
On courbe ensuite ce crénelage comme suit :
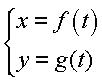 ,
la courbe dentelée est paramétrée par
,
la courbe dentelée est paramétrée par Ci-contre, cas du cercle ; la courbe correspondante, d'équation polaire
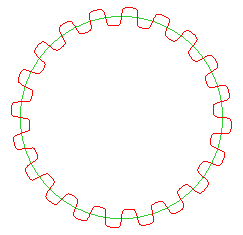
Pour obtenir des dents égales, il faut donc paramétrer par l'abscisse curviligne.

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
DENTELÉE D'UNE COURBE
Notched
curve, gezahnte Kurve
Comment denteler une courbe ?
| Soit h une fonction impaire croissant sur On courbe ensuite ce crénelage comme suit : |
 |
Si la courbe centrale est paramétrée sur 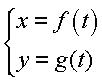 ,
la courbe dentelée est paramétrée par ,
la courbe dentelée est paramétrée par Ci-contre, cas du cercle ; la courbe correspondante, d'équation polaire |
 |
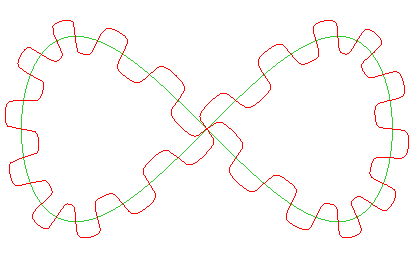
| Si le paramètre t n'est pas proportionnel
à l'abscisse curviligne, les dents ne sont pas de longueurs égales,
comme on le voit ici pour le cas d'un huit.
Pour obtenir des dents égales, il faut donc paramétrer par l'abscisse curviligne. |
 |
| Voici l'exemple de la cycloïde, qui se paramètre facilement par l'abscisse curviligne ; les dents sont bien égales. |  |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2011