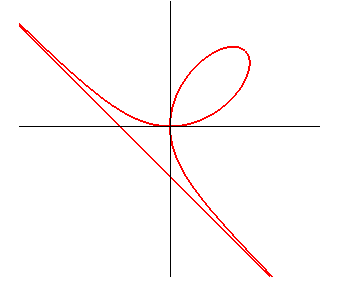Équation cartésienne : . Équation polaire : . Paramétrisation cartésienne : . Cubique rationnelle à point double. L'aire de la boucle est égale à celle du domaine situé entre la courbe et son asymptote (d'équation x + y = –a) ; valeur commune : 3a2/2.

Le folium de Descartes n'est en général pas défini par une propriété géométrique, mais par son équation cartésienne, donnée ci-dessus.
L’équation cartésienne dans un repère tourné de p/4 par rapport au précédent est :  où b = , équation à rapprocher de celle de la trisectrice de Maclaurin : . Le folium de Descartes n’est donc autre que l'image de cette trisectrice dans une dilatation d'axe Ox et de rapport .

Le folium de Descartes est donc aussi une cissoïdale d'ellipse et droite (images par la transformation ci-dessus du cercle et de la droite associés à la trisectrice de Maclaurin), donc une cissoïdale de Zahradnik.

Voir aussi à trident de Newton.
 
 

La surface cubique  coupée par le plan z = 0....

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2007