Équation cartésienne :  où P est un polynôme du troisième degré de valuation nulle. Cubique rationnelle à point double (à l'infini dans la direction de Oy), asymptote à la parabole  et à l'hyperbole . Équation cartésienne réduite :  (cas k = 1 ci-contre).

Les tridents de Newton sont définis par leur équation cartésienne ci-dessus ; on peut les voir comme médianes parallèlement à Oy des paraboles  et hyperboles .	Le trident comme médiane d'une parabole et d'une hyperbole.
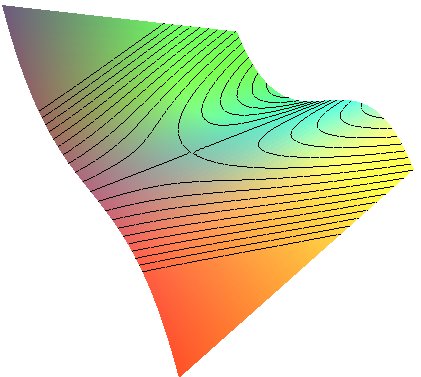
On les retrouve comme courbes de niveau de la surface cubique .

 Ils peuvent aussi être obtenus par hyperbolisme à partir des paraboles cubiques.
 
 

La transformation homographique :  les ramène aux courbes  qui ont leur point double en O. Par exemple, le trident  est transformé en folium de Descartes. Dans la figure ci-contre, nous avons utilisé  au lieu de  pour plus de lisibilité.

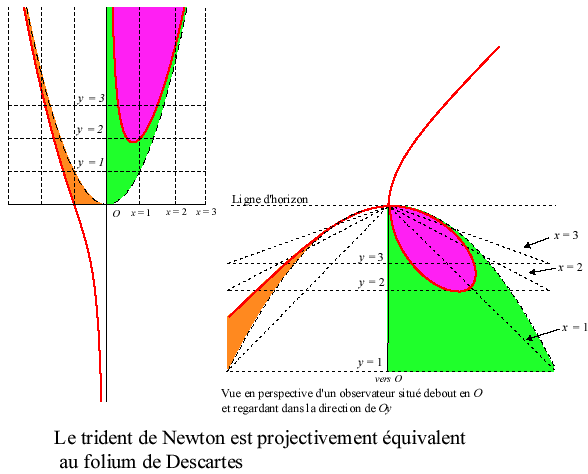
Le folium de Descartes est une perspective du trident de Newton.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2012