Newton trident

NEWTON TRIDENT

Curve studied by Newton in 1701.
Other name: Cartesian parabola.
Isaac Newton (1642-1727): English physicist, mathematician, and astronomer.

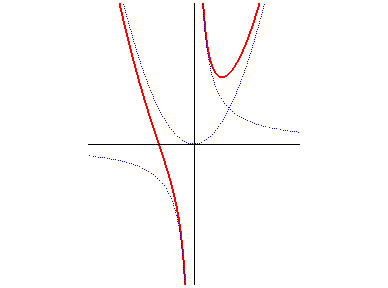Cartesian equation:

where P is a polynomial of degree 3 with valuation 0
Rational cubic with a double point (at infinity in the direction of Oy), the parabola

and the hyperbola

are asymptotes.

Reduced Cartesian equation: (case k = 1 opposite).

The Newton tridents are defined by the above Cartesian equation; they can be seen as the medians along Oy of the parabolas and the hyperbolas .	The trident as the median of a parabola and a hyperbola.
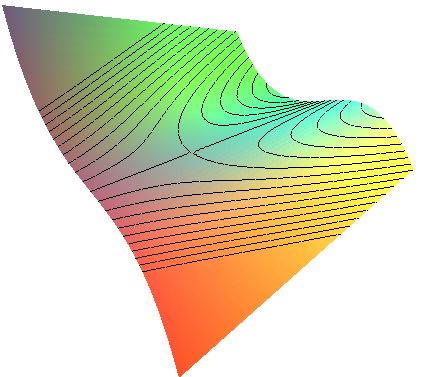
They also appear as contour lines of the cubic surface .

They can also be obtained by hyperbolism from the cubical parabolas.

Their images by the homographic transformation are the curves which have their double point at O. For example, the trident is transformed into a Cartesian folium.
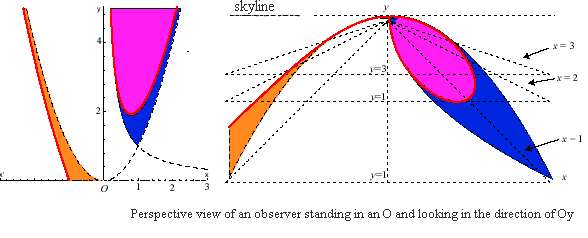
In the opposite figure, we used instead of for the sake of readability.

The Cartesian folium is a perspective of the Newton trident.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra