Courbe étudiée par Loriga en 1910. Juan Jacobo Duran Loriga (1854 - 1911) : mathématicien espagnol. Texeira III p. 52.

Des sources lumineuses ponctuelles identiques étant placées dans le plan, et un point O étant choisi, la courbe de Loriga est le lieu des points du plan où l'éclairement dû aux n sources lumineuses est équivalent à celui qui serait produit par les n sources lumineuses placées en O.

L'éclairement étant inversement proportionnel au carré de la distance à la source, il s'agit donc de la courbe d'équation ponctuelle : .
 

Dans le cas où les n sources sont situées aux sommets d'un polygone régulier de rayon a on obtient pour n = 2, 3, 4 ou 5 :
 
 

n = 2	Hyperbole
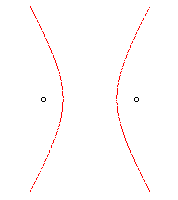n = 3	Quartique de Loriga. Équation  polaire :  . Équation complexe : . Les points d'inflexion se trouvent sur le cercle passant par les sources, avec des tangentes ayant la propriété remarquable visible sur la figure : Comparer avec la quartique de Klein.
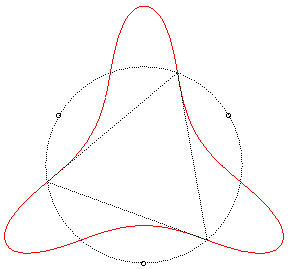n = 4	Sextique de Loriga. Équation polaire :
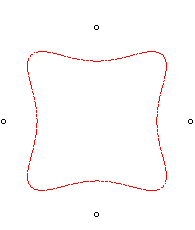n = 5

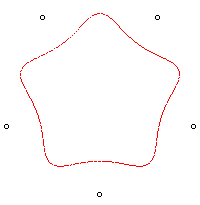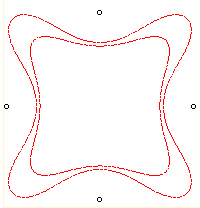
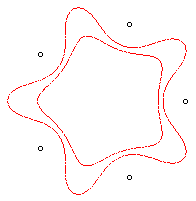
Remarque : la courbe d'équation complexe :  et d'équation polaire :, ne coïncide avec la courbe de Loriga que pour n = 3, comme on le voit sur les figures suivantes :
 

Comparer avec les  courbes isophoniques : et plus généralement, voir les courbes de Goursat.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2011