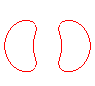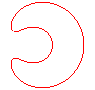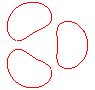FOLIOÏDE
Folioid,
Folioide
Courbe étudiée par P. van Geer en 1918.
Loria 3D p. 240 |
Équation polaire : 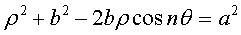 avec
n réel > 0, soit
avec
n réel > 0, soit 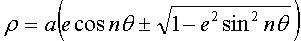 avec
avec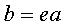 . .
Courbe algébrique
ssi n est rationnel :
si
p et q
sont les numérateur et dénominateur de n, le degré
est 2(p +q) si p et
q sont impairs, et
4(p + q) sinon.
Pour n =1, c'est le cercle de centre (b,
0) et de rayon a.
Pour a = b (e = 1), c'est la rosace
: 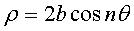 . . |
Cas e < 1 : la courbe est assez proche
d'une double conchoïde
de rosace : 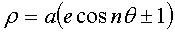 )
:
)
:
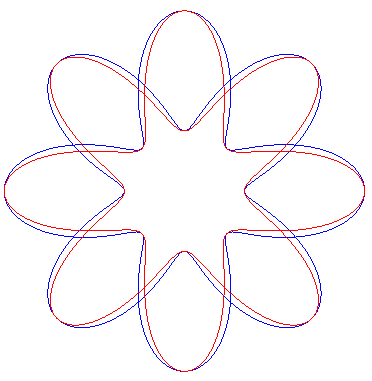 En bleu
les deux conchoïdes de rosace, et en rouge la folioïde, ici pour
n
= 4.
En bleu
les deux conchoïdes de rosace, et en rouge la folioïde, ici pour
n
= 4.
Cas e > 1 : la courbe est formée de p
courbes fermées si p et q sont impairs, et 2p
sinon.

n = 1 : cercle
|
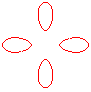
n = 2
|

n = 3
|
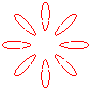
n = 4
|

n = 5
|
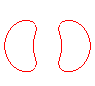
n = 1/2
|
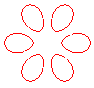
n = 3/2
|

n = 5/2
|

n = 7/2
|

n = 9/2
|

n = 1/3
|
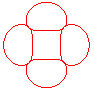
n = 2/3
|
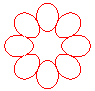
n = 4/3
|

n = 5/3
|

n = 7/3
|

n = 1/4
|
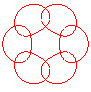
n = 3/4
|
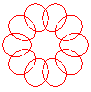
n = 5/4
|
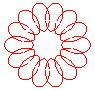
n = 7/4
|

n = 9/4
|
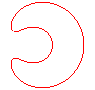
n = 1/5
|
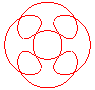
n = 2/5
|
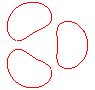
n = 3/5
|
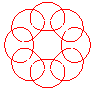
n = 4/5
|
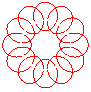
n = 6/5
|
Si l'on enroule le plan du cercle 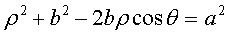 en un cône
de sommet O et de demi-angle au sommet
en un cône
de sommet O et de demi-angle au sommet 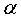 ,
d'axe Oz, la projection sur xOy de ce cercle enroulé
est la folioïde :
,
d'axe Oz, la projection sur xOy de ce cercle enroulé
est la folioïde : 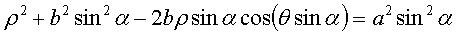 ,
ce qui fournit une construction de ces dernières à partir
d'un simple cercle dans le cas n < 1.
,
ce qui fournit une construction de ces dernières à partir
d'un simple cercle dans le cas n < 1.
© Robert FERRÉOL
2016
 En bleu
les deux conchoïdes de rosace, et en rouge la folioïde, ici pour
n
= 4.
En bleu
les deux conchoïdes de rosace, et en rouge la folioïde, ici pour
n
= 4.