Équation cartésienne : . Quartique rationnelle. Équation polaire : . Pour a > b  : équation polaire  avec  et . Pour 0 < a < b : équation polaire  avec  et .

La courbe d'Alain est la courbe définie par l'équation cartésienne ci-dessus.
Voici ses différentes allures :
 

cas b = 0	cas 0 < b < a
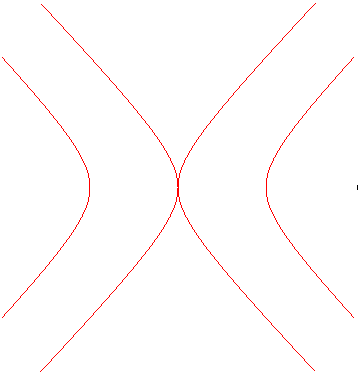
Réunion des deux hyperboles .
cas b = a	cas  b > a > 0
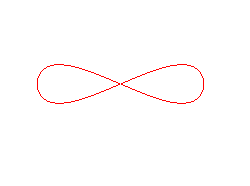
Hyperbole  et ses asymptotes.	Lemniscate cylindrique.

 

La courbe d'Alain est la projection sur le plan xOy de l'intersection du cône elliptique : avec le paraboloïde hyperbolique :.

 

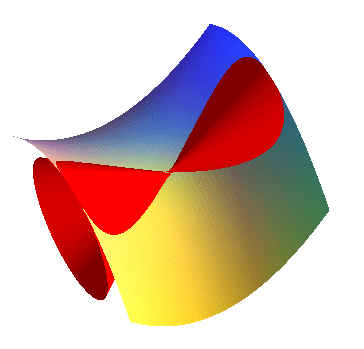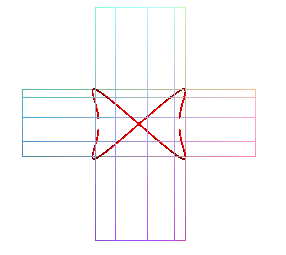
Dans le cas a < b, cette courbe est aussi la projection plane de l'intersection de deux cylindres de révolution à plan tangent en commun, le plan de projection étant ce plan commun. Plus précisément, la projection sur le plan xOy des cylindres  avec  est la courbe d'équation . .

Voir aussi les courbes de Booth, images des précédentes par une affinité complexe.
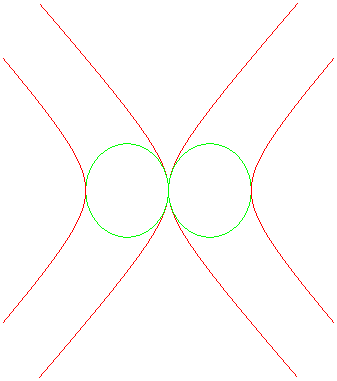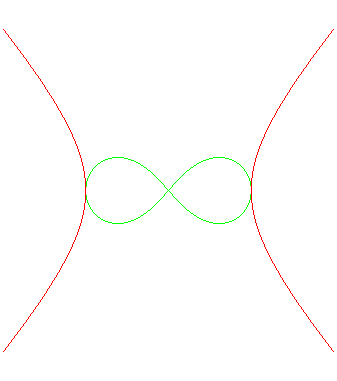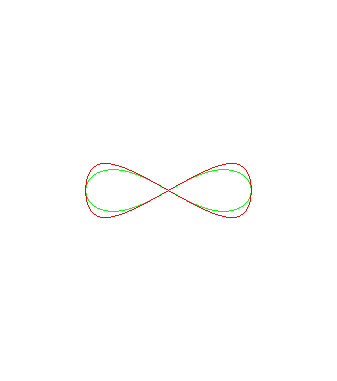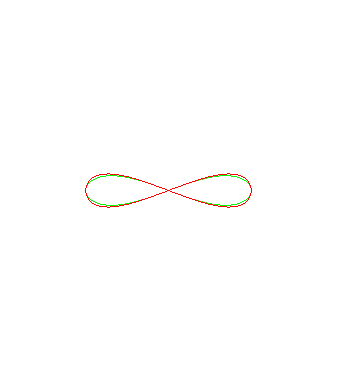
Ci-dessous, animation des courbes d'Alain , en rouge, avec les lemniscates de Booth , en vert.

© Robert FERRÉOL  2016