Équation polaire :  (ou  ) avec n réel > 0.

Ls nœuds sont les transformées de Brocard du kappa, le pôle étant situé sur le centre du kappa.
Chaque courbe est formée d'une branche infinie de base obtenue pour  :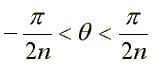

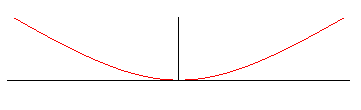
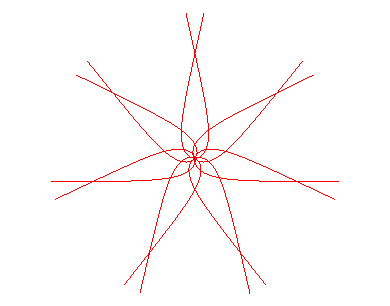
et de toutes ses images par des rotations d'angle  pour k entier.

Si n est rationnel de numérateur p, et de dénominateur q, la courbe est formée de 2p branches images de la branche de base par rotation lorsque q est impair, et de p branches lorsqu'il est pair.

Exemples :

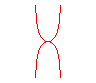
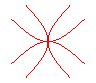
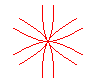
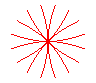
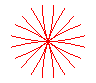
n = 1 : kappa	n  = 2 : moulin à vent	n = 3	n = 4	n = 5
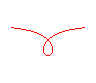
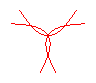
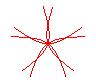
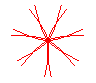
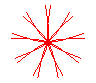
n = 1/2 : strophoïde droite	n = 3/2	n = 5/2	n = 7/2	n = 9/2
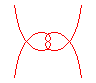
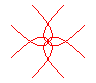
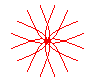
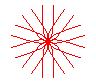
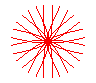
n  = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
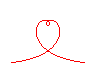
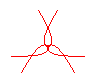
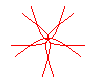
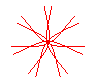
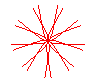
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
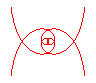
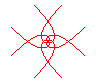
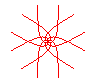
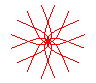
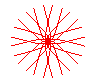
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Tout nœud est une stéréographique de clélie.
L’inverse (de centre O et de rapport a²) d'un nœud est la même courbe tournée de .
Ligne asymptotique d'hélicoïde gauche ????

Comparer avec les épis.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2015