Horoptère

Courbe étudiée par Helmholtz, Ludwig, Schur en 1902.
Nom masculin, du grec horos "limite" et optêr "observateur".
Autre nom : cercle cubique.
Voir sur wikipedia une définition plus générale de cette courbe en optique physiologique.

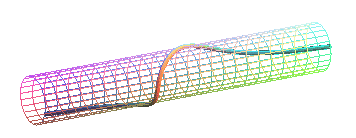
Système d’équations cartésiennes : .
Paramétrisation cartésienne : , ou, en faisant t : = tan (t / 2) : .
Cubique 3D:rationnelle.

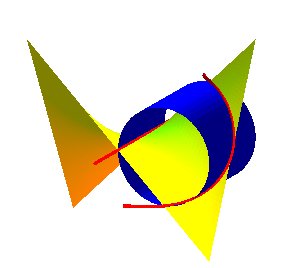
L’horoptère est l’intersection du cylindre de révolution d'axe : et passant par O avec chacun des deux paraboloïdes hyperboliques équilatères d'équations et .
On élimine de cette intersection la droite Oy dans le premier cas, et la droite dans le deuxième cas, droite qui est commune aux deux quadriques.
L'horoptère est donc évidemment aussi l'intersection des deux PH susmentionnés.

La paramétrisation cartésienne montre que l'horoptère est une couronne tangentoïdale ; lorsqu'on développe le cylindre sur lequel il est tracé, on obtient donc une tangentoïde.

Les projections sur les plans xOy, xOz et yOz sont respectivement la cubique d'Agnesi : , le cercle : et l'anguinée :.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres