Curve studied by Helmholtz, Ludwig and Schur in 1902. From the Greek horos "limit" and opter "observer". Other name: cubic circle. See on wikipedia a more general definition of this curve in the study of binocular vision.

 

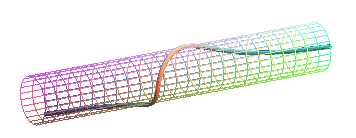
System of Cartesian equations: . Cartesian parametrization: , or, with t : = tan (t / 2): . Rational 3D cubic.

 

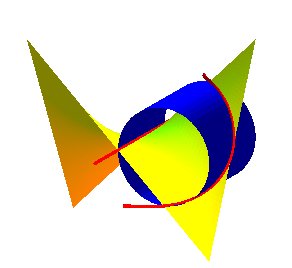
The horopter curve is the intersection between the cylinder of revolution with axis x = a, z = 0 and passing by O and the two rectangular hyperbolic paraboloids with of equation  and . We take out from this intersection the line Oy in the first case, and the line x= 2a, y=0 in the second case, this line being common to both the quadrics. The horopter curve is obviously also the intersection between the two aforementioned hyperbolic paraboloids.

The Cartesian parametrization shows that the horopter curve is a cylindrical tangent wave; when the cylinder on which it is traced is developed, we get a tangentoid.

The projections on the planes xOy, xOz and yOz are the witch of Agnesi, the circle  and the anguinea, respectively.
 
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2018