CUBIQUE DE HUMBERT
Humbert
cubic, Humbertsche Kubik
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CUBIQUE DE HUMBERT
Humbert
cubic, Humbertsche Kubik

| Courbe étudiée par G. Humbert en 1887 (j.
de math pures et appliquées, 1887, p. 377).
Marie Georges Humbert (1859-1921) : mathématicien français. Nom maison. |
| Équation polaire : Equation cartésienne : Cubique elliptique. Abscisse curviligne donnée par |
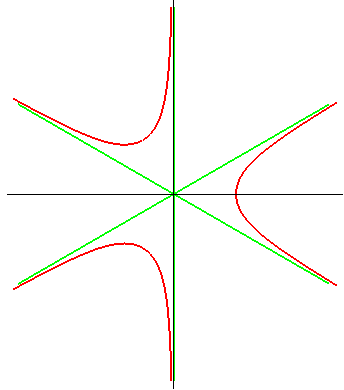 |
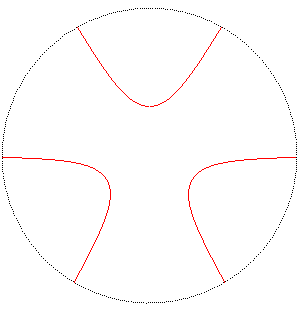
La cubique de Humbert est la courbe définie par
les équations ci-dessus.
Son équation polaire montre que c'est un cas particulier
de spirale sinusoïdale
(paramètre n = –3).
Son équation cartésienne montre que c'est
un cas particulier d'hyperbole
cubique.
Ele est l'inverse de la courbe de Kiepert.
Elle a été considérée par
Humbert car c'est l'une des rares cubiques, avec la cubique
de Tschirnhausen, pour lesquelles
s'exprime rationnellement en fonction de x et y (mais pas
en fonction de x seul !).
La cubique de Humbert et le trêfle
équilatère (de forme similaire, mais dont les asymptotes
sont non concourantes) sont les seules cubiques ayant une symétrie
de rotation d'ordre 3 (voir à courbe
de Goursat).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013