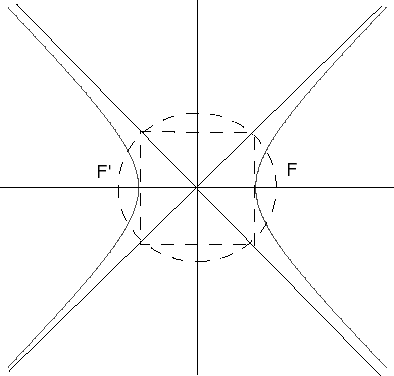Équation cartésienne réduite : . Dans le repère tourné d'un huitième de tour : (a  = demi-axe focal). Foyers : F(, 0) et F'(–, 0). Directrices : droites d'équation x =  et x = – .

Paramétrisation cartésienne :  (avec  ; forme choisie dans la suite). ou  (avec  ). Équation polaire :  (c'est donc un cas particulier de spirale sinusoïdale). Equation polaire générale d'une hyperbole équilatère passant par O : (en complexes : ) Abscisse curviligne : . Rayon de courbure : . Équation bifocale : . Équation tripolaire : MF.MF' = OM2, O étant le milieu de [FF']. Équation polaire (pôle F, axe Fx) : .

tion

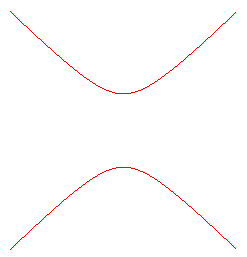
L' hyperbole équilatère est l'hyperbole à axes (ou asymptotes) perpendiculaires, ou d'excentricité . Elle est aux hyperboles générales ce qu'est le cercle aux ellipses.

En voici diverses définitions géométriques :
 

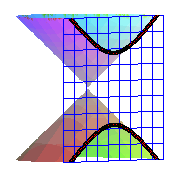
1) Définition conique : L'hyperbole équilatère est la section d'un cône de révolution équilatère (angle au sommet de 90°) par un plan strictement parallèle à l'axe du cône.

2) Définition bifocale :
L'hyperbole équilatère est le lieu d'un point dont la différence des distances à deux points fixes F et F' est égale à  fois la distance entre ces deux points (voir l’équation bifocale ci-dessus).

3) Définition par foyer et directrice :
L'hyperbole équilatère est le lieu d’un point M tels que  où H est le projeté de M sur la directrice (D).

4) Définition cissoïdale :
   Étant donné deux droites perpendiculaires et un point A en dehors de ces droites, le lieu des points M tels que  où P et Q sont les deux points d'intersection avec les deux droites d'une droite variable passant par A, est l'hyperbole passant par A et d'asymptotes les deux droites de départ  (on en déduit facilement que l’hyperbole est la cissoïdale de deux droites perpendiculaires).

5) a) Définition angulaire (cas particulier de stelloïde) :

Étant donnés deux points distincts A et B, le lieu des points M tels que les bissectrices des droites (MA) et (MB) aient des directions constantes est l'hyperbole équilatère passant par A et B dont les asymptotes passent par le milieu de [AB] et sont parallèles à ces directions constantes. Interprétation mécanique * : une corde est attachée à une extrémité à un point fixe A, passe par une poulie B et est maintenue à la main à l'autre extrémité. Un seau est suspendu à la corde par une poulie entre A et B. Le seau décrit une portion d'hyperbole équilatère.  * Voir Roguet p 161 (1842)

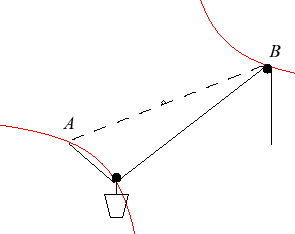La courbe du seau d'eau : comparer avec la courbe du danseur de corde.

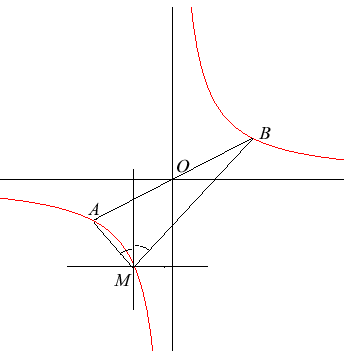
 5) b) Définition angulaire équivalente à la précédente.

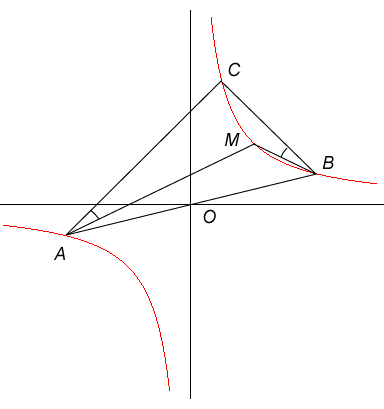
Etant donné trois points distincts A,B,C, le lieu des points M vérifiant (AC, AM) = (BM, BC)   (1) (angles orientés de droites) est l'unique hyperbole équilatère de diamètre [AB] (i.e. centrée au milieu de (A,B)), éventuellement dégénérée, passant par C. Les asymptotes sont parallèles aux bissectrices de (AC) et (BC). (1) s'écrivant aussi : (AB, AM) – (BM, AB) = (AB, AC) – (BC, AB), on peut donner une troisième définition angulaire : étant donné deux points distincts A,B, et un réel  le lieu des points M vérifiant mesure(AB, AM) – mesure(BM, AB)  =   mod  est une hyperbole équilatère de diamètre [AB] . Par exemple, mesure(AB, AM) – mesure(BM, AB)  =  mod   donne  l'hyperbole équilatère de sommets A et B. Dit autrement, l'hyperbole équilatère de sommets A et B est le lieu du sommet M d'un triangle (AMB) vérifiant .

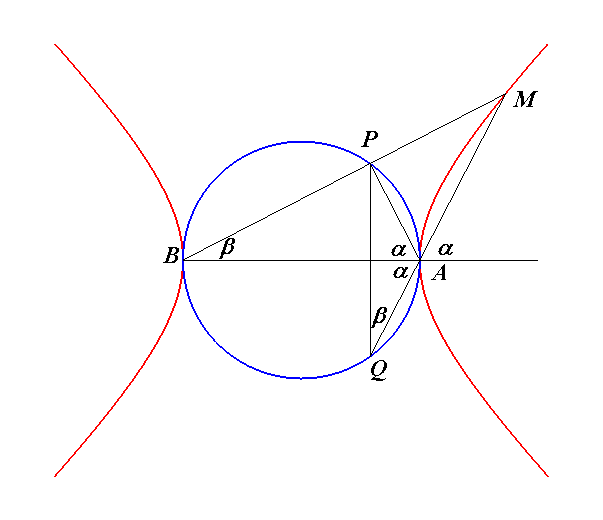
La définition précédente permet la construction ci-contre [J. Lemaire, hyperbole équilatère, p. 1] de l'hyperbole équilatère de sommets A et B à partir du cercle de diamètre [AB]. Le point P parcourant le cercle, les angles  vérifient et on a bien, dans le cas de la figure où , pour le triangle (AMB) : . Le point M décrit ici une branche de l'hyperbole, l'autre branche étant obtenue pour . Analytiquement, avec A(a, 0) et B(-a, 0), la transformation  est définie par  (homologie harmonique de centre B et d'axe x = a), donc le cercle  est bien transformé en l'hyperbole .

6) Définition strophoïdale :
 

L'hyperbole équilatère est la courbe strophoïdale d'une droite (D) relativement à un point O en dehors de (D) et un point A situé à l'infini sur une perpendiculaire à (D).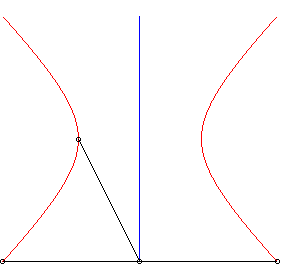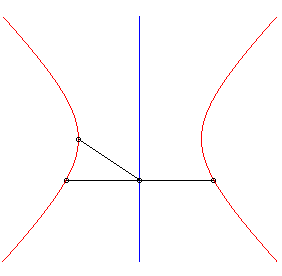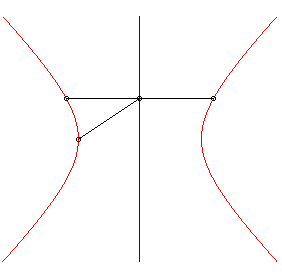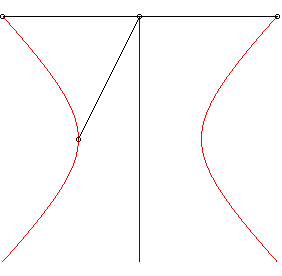

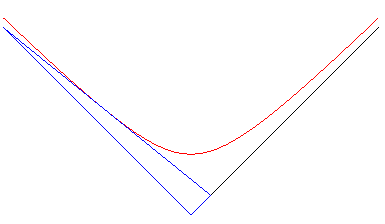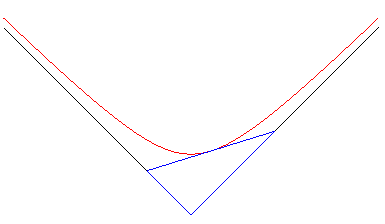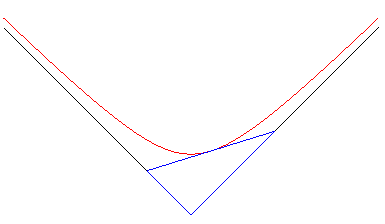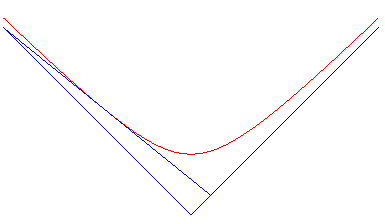
7) Définition comme enveloppe d'un triangle d'aire constante.
 

L'hyperbole équilatère est l'enveloppe d'un segment [AB] dont les extrémités se déplacent sur les axes orthogonaux Ox et Oy de sorte que le triangle OAB orienté ait une aire constante. Le point de contact est le milieu de [AB]. Si donc on considère un récipient cubique rempli d'un liquide coloré dont une arête reste horizontale, la trace laissée par le liquide sur les bords lorsqu'on pivotera le récipient autour de cette arête sera limitée par une hyperbole.  Cette propriété est conservée dans le cas de deux droites non orthogonales ; l'enveloppe est une hyperbole quelconque. La généralisation 3d de ce problème donne la surface xyz = cte.

 

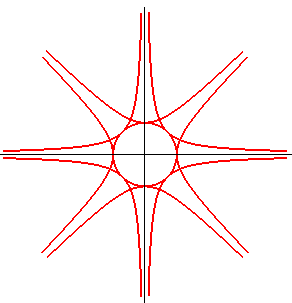
Figure montrant les 4 hyperboles équilatères  et , accompagnées du cercle .

 

Voir aussi la chaînette conique, la trompette de Gabriel et les hyperboloïdes.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2024