Courbe étudiée par Lucas en 1879. Autre nom : courbe halysique. [brocard partie comp. , loria p521]

 

Équation multipolaire : . Courbe algébrique de degré 2n. Les stelloïdes et les cassiniennes et les sont les images réciproques des lignes de coordonnées par la fonction complexe f définie par .

les  étant n points fixes du plan, les stelloïdes de pôles les  sont les lieux des points M du plan telles que la moyenne des angles que font les droites  où avec une direction fixe, est constante. Les courbes ne dépendent pas de la direction fixe choisie.

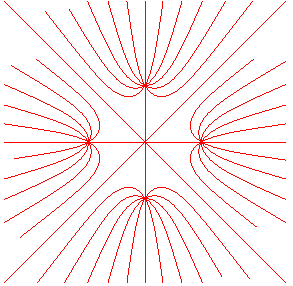
Les stelloïdes ne sont autres que les trajectoires orthogonales des cassiniennes de mêmes pôles.

Le cas n = 2 donne l'hyperbole équilatère, trajectoire orthogonale des ovales de Cassini.

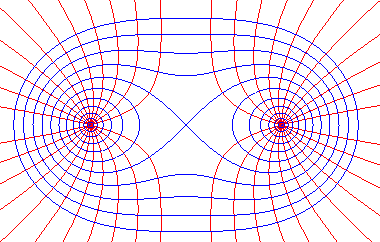
Les équipotentielles du champ magnétique créé par n fils parallèles parcourus par un courant de même intensité et de même sens sont, dans chaque plan orthogonal aux fils, les stelloïdes de foyers les points d'intersection avec les fils ; idem pour les lignes de champ du champ électrostatique créé par n fils parallèles uniformément chargés avec des charges identiques.

On peut généraliser ces courbes à des moyennes pondérées, autrement dit, ayant une équation multipolaire du type :  ; ces courbes s'obtiennent physiquement comme équipotentielles de champ magnétiques avec des fils parcourus par des courants des distincts, ou comme lignes de champ électrostatiques avec des fils ayant des charges distinctes.

Par exemple, pour n = 2 et , on obtient un faisceau de cercles à points de bases les pôles.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2016