1) Dans un repère de centre le centre du cercle Équation polaire : . Équation cartésienne :  . Conique. Paramétrisation cartésienne :   (). Paramétrisation cartésienne rationnelle :   (). Abscisse curviligne : . Angle tangentiel polaire : . Rayon de courbure, équation intrinsèque 1 : . Équation intrinsèque 2 :   (ici  ) Longueur :  ; aire : .

 

2) Équation cartésienne générale :  (non vide ssi ) Équation cartésienne du cercle de centre  et de rayon R : . Paramétrisation cartésienne : . Équation polaire : , ou  se réduisant à  si le cercle passe par O.

 

3) Dans un repère centré sur le cercle, équation polaire réduite :  (rosace). Abscisse curviligne : . Angle tangentiel polaire : . Aire de la zone obtenue pour  : .

Un cercle est le lieu formé des points du plan équidistants d'un point fixe.
Il peut être défini comme "conique circulaire" ou "conique propre d’excentricité nulle", ou "courbe à courbure constante et torsion nulle".

Cinématiquement, les cercles sont les trajectoires des mouvements à vitesse angulaire constante. En effet,  a pour solutions  et .

Les courbes à normale constante (N = cte, cf. notations) sont les cercles centré sur Ox (plus les droites parallèles à Ox).

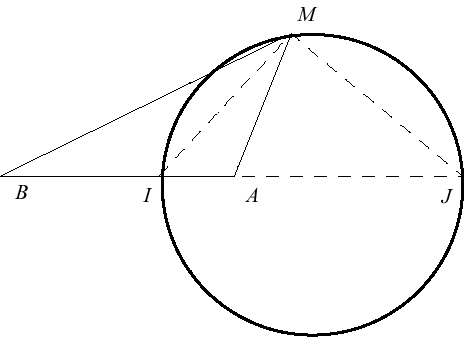
Etant donnés deux points distincts A et B, le lieu des points M tel que l'angle de droites (MA, MB) est constant est un cercle dont est une corde [AB] (isoptique du segment [AB]).
 

Le lieu des points M vérifiant  est (sauf pour k = 1) le cercle (dit d'Apollonius) de diamètre [I J] où I et J sont les deux points de (AB) vérifiant  ; les droites (MI) et (MJ) sont les bissectrices de l'angle AMB. Les points A et B sont inverses par rapport à ce cercle. Le cercle d'Apollonius est donc aussi le lieu des points M voyant les segments [AI] et [BI] sous le même angle ((MA,MI)=(MI,MB)) ; idem pour [AJ] et [BJ]. Voir ce site. NB : ne pas confondre avec les cercles d'Apollonius associés à 3 cercles (cf. ci-dessous).
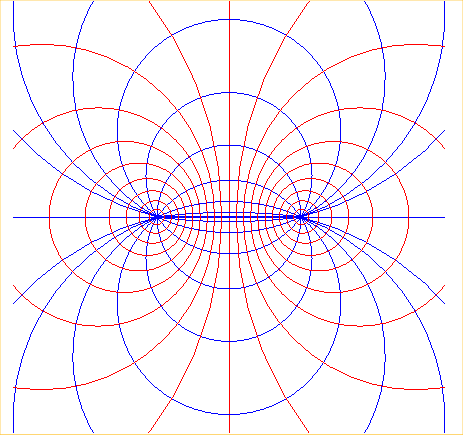
Pour k variant, ces cercles forment un faisceau de cercles à points limites A et B ; le faisceau conjugué est l'ensemble des cercles passant par A et B  (dit, à points de base A et B) et chaque faisceau est l'ensemble des cercles orthogonaux à l'un des cercles de l'autre faisceau. Cette figure s'interprète comme formée de lignes de champ magnétiques ou électrostatique ; voir ici. Voir aussi les figures d'interférences d'ondes circulaires à la fiche coniques.
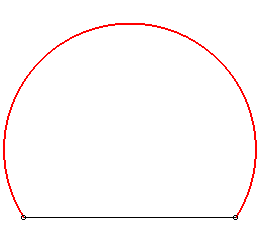
Le cercle est aussi la solution du problème isopérimétrique : trouver la courbe fermée simple de longueur donnée qui enserre une aire maximale (ou de longueur minimale pour une aire donnée). De même, l'arc de courbe de longueur donnée L joignant deux points donnés A et B, situé dans un demi plan délimité par (AB) et enserrant la plus grande aire dans ce demi-plan est l'un des 2 arcs de cercle de longueur L joignant A à B  (à vérifier : si on cherche la zone dont le centre de gravité est le plus éloigné de (AB), c'est alors un arc de chaînette).

 
 

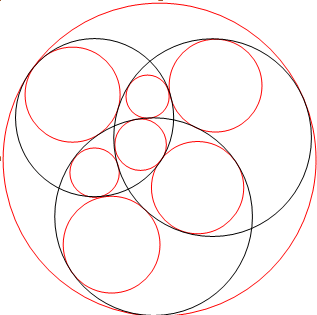
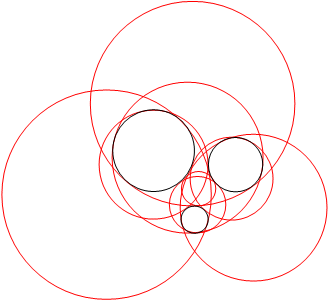
Un autre problème célèbre concernant les cercles, posé déjà par Apollonius, est celui de déterminer les cercles tangents à 3 cercles donnés ; il y a en général 8 solutions comme dans les exemples ci-contre, mais seulement 2 lorsque les 3 cercles sont tangents deux à deux (voir la baderne d'Apollonius).

Voir aussi les courbes à accélération angulaire constante, les cercles géodésiques, tracés sur des surfaces, et les cercles gauches.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2020