Courbe strophoïdale

COURBE STROPHOÏDALE
Strophoidal curve, strophoidale Kurve

Dans le cas où la courbe de départ est une droite, notion étudiée par M. Lagrange en 1900.
Du grec strophos "cordon, ceinture, torsade".

Pour une courbe de départ d'équation polaire dans le repère (F, , ) et le point O de coordonnées (a, b) dans ce repère :
équation polaire dans le repère (F, , ) : .

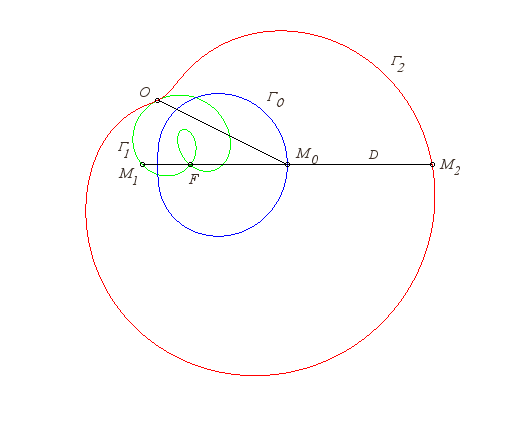
La (courbe) strophoïdale d'une courbe de pôle O et de point fixe F est le lieu des points M d'une droite variable (D) passant par F tels que M₀M = M₀O où M₀ est un point d'intersection (autre que F) de la droite (D) avec la courbe .
Autrement dit, c'est le lieu des intersections d'un cercle centré en M₀ sur la courbe et passant par O, avec la droite (FM₀).
La strophoïdale est donc formée de deux branches et dont est la médiane de pôle O.
M₀M₁=M₀M₂ = M₀O

Lorsque la courbe est une droite, O un point de cette droite et F un point extérieur à cette droite, les strophoïdales correspondantes sont les strophoïdes (droite lorsque (OF) est perpendiculaire à la droite ).

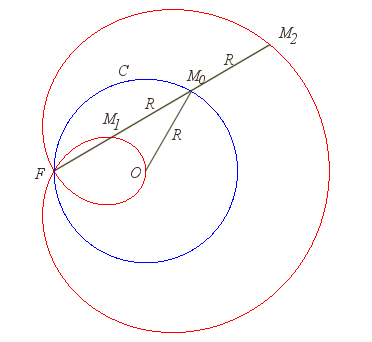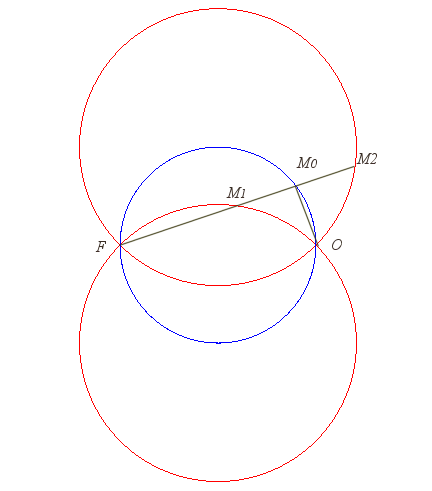
Lorsque la courbe est un cercle, O son centre, la strophoïdale est la conchoïde de de pôle F et de module le rayon du cercle ; en particulier, lorsque F est sur le cercle, on obtient le limaçon trisecteur.

Construction de la strophoïdale d'un cercle, dans le cas où O est sur le cercle et F aligné avec O et le centre du cercle.
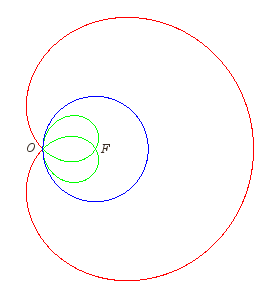
Lorsque F est au centre du cercle, la strophoïdale est la néphroïde de Freeth.
Lorsque F va à l'infini, la strophoïdale tend vers une torpille (voir ci-dessous).

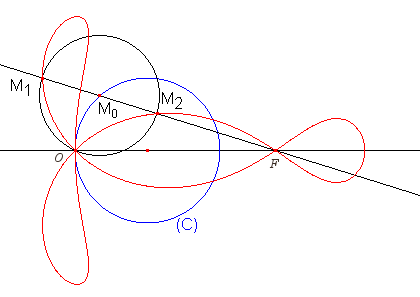
Lorsque F est diamétralement opposé à O, la strophoïdale se réduit à deux cercles, centrés sur le cercle de départ, et de rayon (à justifier géométriquement !).

GÉNÉRALISATIONS

1) le point F est placé à l'infini.

La (courbe) strophoïdale d'une courbe de pôle O relativement à une direction de droite D est le lieu des intersections d'un cercle centré en M₀ sur la courbe et passant par O, avec la parallèle à D passant par M₀ .
La transformation associée est alors parfois appelée "transformation de Brocard", ce dernier l'ayant étudiée dans le cas particulier du cercle.

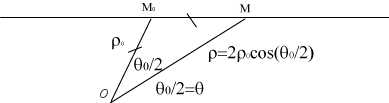
Pour une direction de droite Ox et pour une courbe de départ d'équation polaire dans le repère (O, , ) : , la strophoïdale est la réunion des deux courbes d'équation polaire et .
Ci-contre, construction de l'une des deux branches.

Exemples :

Lorsque la courbe est une droite, et O un point en dehors de cette droite, on obtient les hyperboles (voir ci-contre le cas où la droite est perpendiculaire à (Ox)).

Lorsque la courbe est un cercle, et O un point de ce cercle (équation ), la strophoïdale est le trifolium : . Voir ci-contre le cas où le cercle est centré sur Ox, ce qui donne la torpille. Lorsque le cercle est centré sur Oy, on obtient le bifolium régulier.

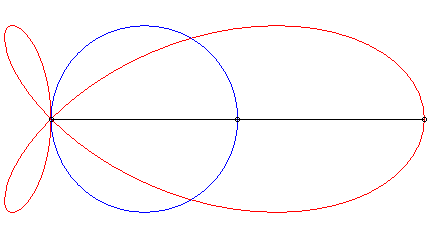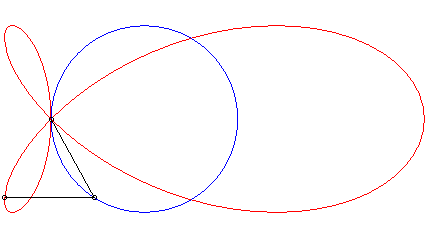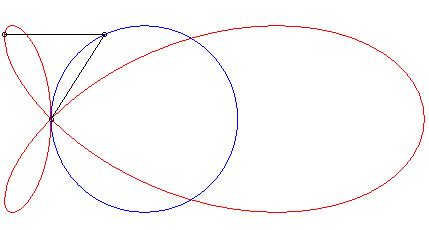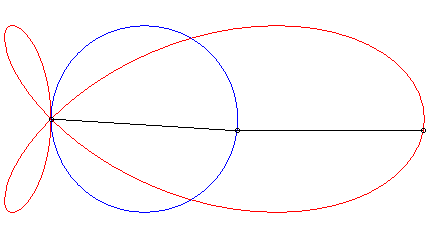Lorsque la courbe de départ est une parabole de foyer O et de paramètre p, la direction de droite l'axe de la parabole, l'une des branches de la strophoïdale n'est autre que la directrice, et l'autre, une parabole de sommet O et de paramètre p/2.

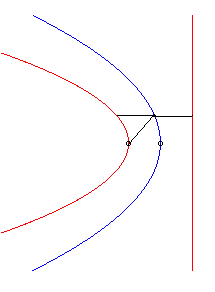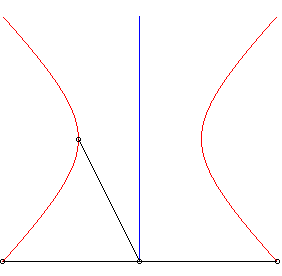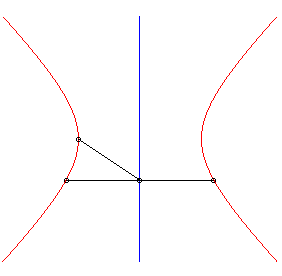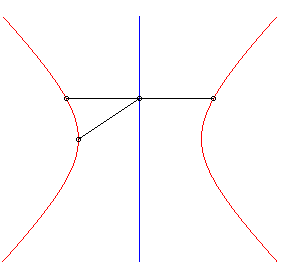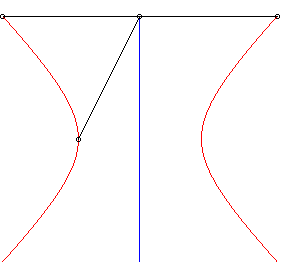
Lorsque la courbe de départ est une ellipse de foyer O et la direction de droite un axe de l'ellipse, la strophoïdale est formée de deux autres ellipses, de sommets O.
Phénomène similaire pour les hyperboles.

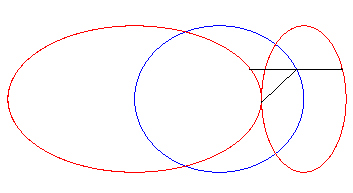Lorsque la courbe de départ est une spirale hyperbolique , la strophoïdale "de droite" est une syncochléoïde, et celle "de gauche" (en vert), une cochléoïde : .

1) le point O est remplacé par une courbe (idée de Pierre Daniel).

La (courbe) strophoïdale d'une courbe de point fixe F relativement à une courbe est le lieu des intersections d'un cercle centré en M₀ sur la courbe et tangent à la courbe , avec la droite (FM₀).

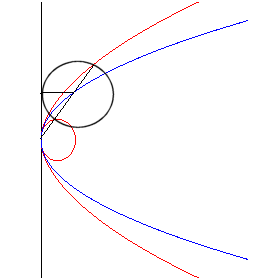
Voici un cas particulier simple : celui où la courbe est une droite passant par F.

Prenant l'axe Fy comme droite et pour une courbe de départ d'équation polaire dans le repère (F, , ) : , la strophoïdale a pour équation polaire .
Ci-contre, exemple de la parabole ; la strophoïdale a pour équation : ; c'est une conchoïde focale de la parabole .

Autre exemple :

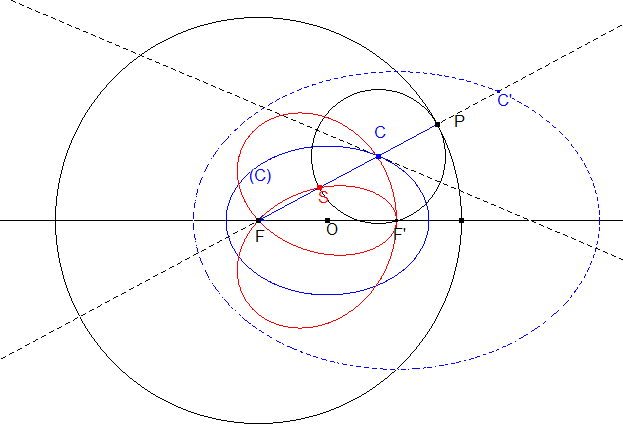
La strophoïdale d'une ellipse (C) de point fixe un de ses foyers F, relativement à son cercle directeur centré en F, est composée du cercle directeur lui-même, et de la conchoïde, de pôle F et de paramètre 2a, d'une conique homothétique de la première dans l'homothétie de centre F et de rapport 2 (en effet, avec les notations de la figure :
FS = FC – CP = 2FC – 2a = FC' – 2a.).
Cette strophoïdale est donc une courbe de Jerabek.
Même phénomène dans le cas d'une hyperbole.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Lorsque la courbe est une droite, et O un point en dehors de cette droite, on obtient les hyperboles (voir ci-contre le cas où la droite est perpendiculaire à (Ox)).
Lorsque la courbe est un cercle, et O un point de ce cercle (équation ), la strophoïdale est le trifolium : . Voir ci-contre le cas où le cercle est centré sur Ox, ce qui donne la torpille. Lorsque le cercle est centré sur Oy, on obtient le bifolium régulier.
Lorsque la courbe de départ est une parabole de foyer O et de paramètre p, la direction de droite l'axe de la parabole, l'une des branches de la strophoïdale n'est autre que la directrice, et l'autre, une parabole de sommet O et de paramètre p/2.
Lorsque la courbe de départ est une ellipse de foyer O et la direction de droite un axe de l'ellipse, la strophoïdale est formée de deux autres ellipses, de sommets O. Phénomène similaire pour les hyperboles.
Lorsque la courbe de départ est une spirale hyperbolique , la strophoïdale "de droite" est une syncochléoïde, et celle "de gauche" (en vert), une cochléoïde : .