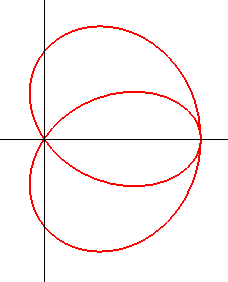Équation polaire : . Pour 0 < k = tha  <1 : . Pour k = cotha  > 1 : . Équation cartésienne : . Équation polaire dans le repère de centre (a,0) : Quartique rationnelle circulaire.

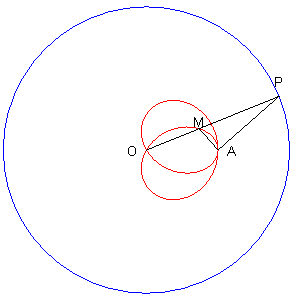
La courbe de Jerabek  est le lieu de l'extrémité M d'un angle droit PAM, le point P décrivant un cercle (C) de centre O et de rayon a, et le point M appartenant à la droite (OP) (ici, A(a, 0) et OP = ka). C'est donc la base du mouvement du plan dont P est un point fixe, et (PA) une droite fixe, mouvement dit conchoïdal circulaire.

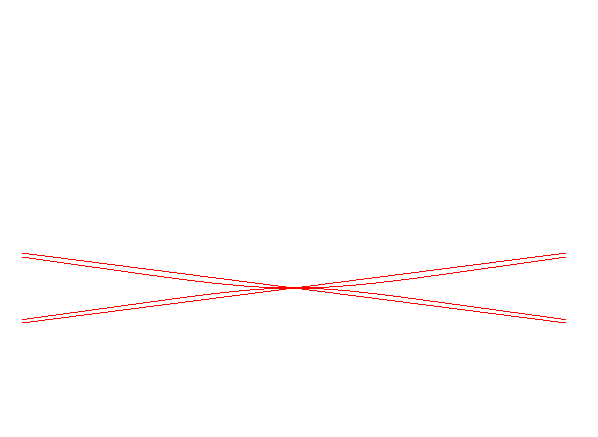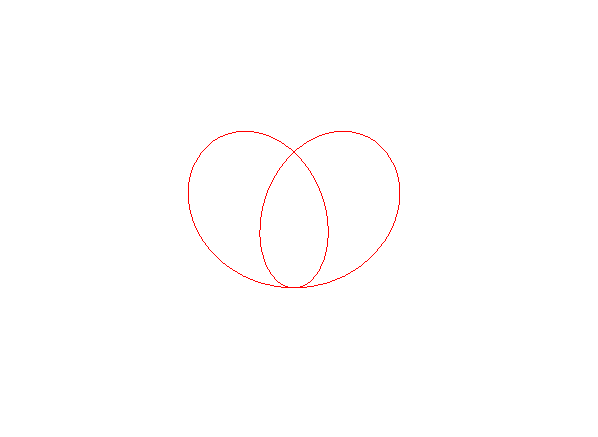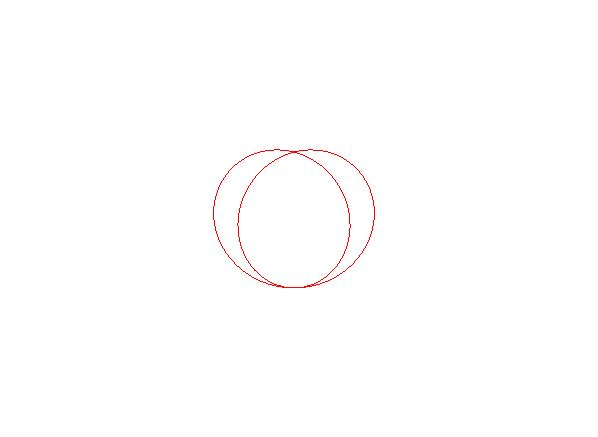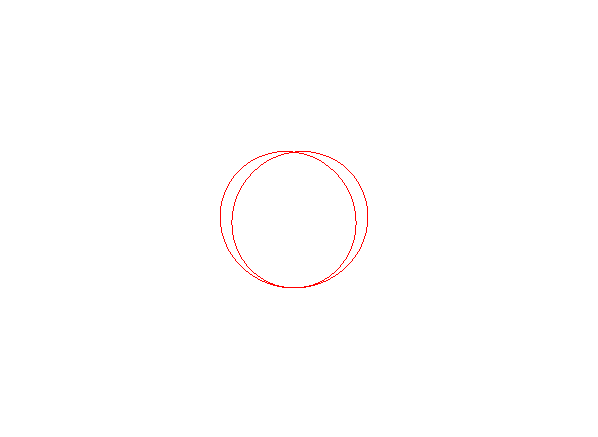
Lorsque A est à l'intérieur du cercle (k > 1), la courbe est fermée, incluse dans le cercle, et possède un point double crunodal et un point double tacnodal.

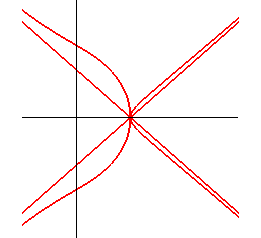
Lorsque A est à l'extérieur, il y a un point double tacnodal et deux asymptotes.

D'ailleurs, ces deux cas sont inverses l'un de l'autre : plus précisément les courbes  et  sont inverses par rapport au cercle (C).

L'équation polaire mise sous la forme  où e = 1/k, montre que la courbe de Jerabek est une conchoïde de conique à centre de pôle un foyer de cette conique, de module le demi-grand axe (voir à conchoïde de conique).

C'est aussi une podaire de développée de conique à centre par rapport à l'un des foyers.
 
 

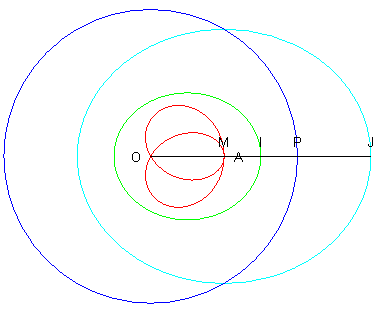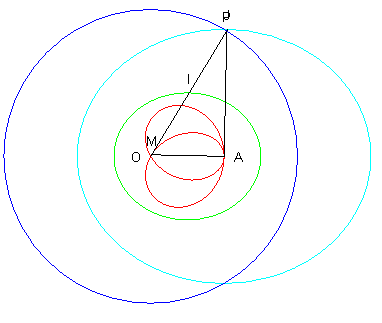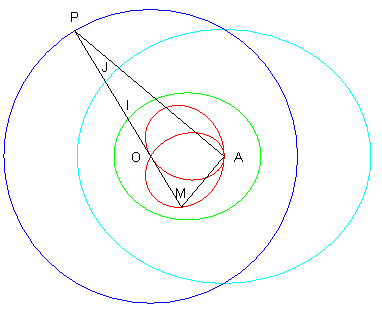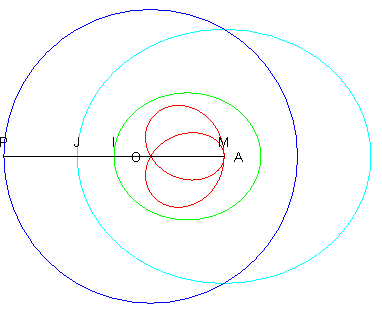
Quand A est à l'intérieur du cercle, si I est le milieu de [MP] , IM = IP = IA, donc OI + IA = OP = cte : le point I décrit une ellipse et la courbe de Jerabek s'obtient en diminuant le rayon vecteur de l'ellipse verte mené du foyer O, d'une longueur égale au rayon vecteur qui aboutit à l'autre foyer A. Soit I l'image de I dans l'homothétie de centre O et de rapport 2 ; J décrit l'ellipse bleue et JM = OP = cte : la courbe de Jerabek est la conchoïde de l'ellipse bleue par rapport au foyer O, le rayon vecteur étant diminué du demi-grand axe de cette ellipse. M est symétrique de A par raport à la normale menée par I à l'ellipse verte : la courbe de Jerabek est donc l'orthotomique de pôle A de la développée de l'ellipse verte. Voir à strophoïdale, une construction strophoïdale de la courbe de Jerabek utlisant cette propriété.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2016