Équation polaire :  où  est celle de la courbe de départ.

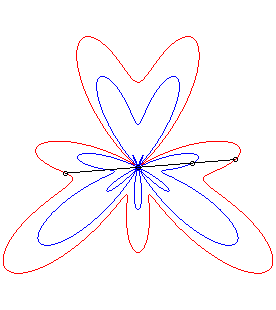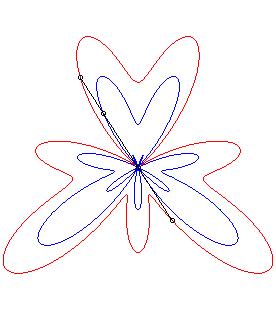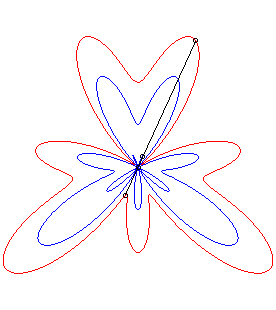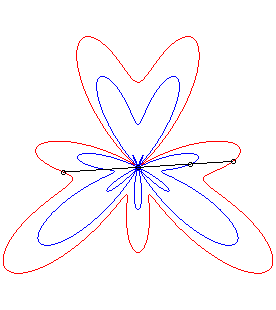
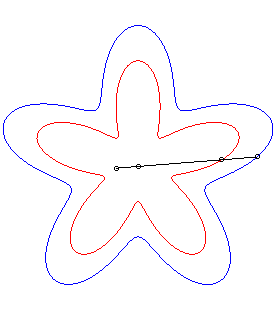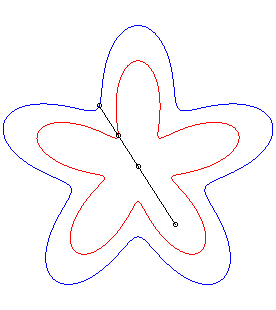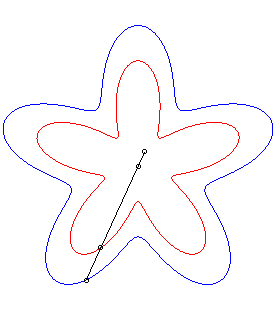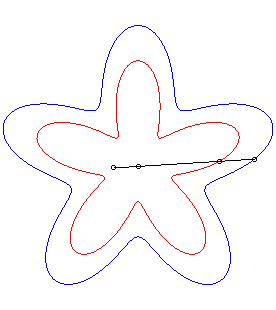
La conchoïde d'une courbe  de pôle O (ou par rapport à O) et de module a (algébrique) est le lieu des points M de la droite orientée (OM0) tels que , où M0 décrit . Par exemple, la courbe décrite par un chien tirant sur sa laisse de longueur a en direction d'un chat situé en O, le maître décrivant la courbe , est la conchoïde de cette dernière, de module –a. Ou bien, une barre rigide coulissant le long d'un point O a l'un de ses points assujetti à décrire la courbe  : tous les points de cette barre décrivent des conchoïdes de . La notion générale est celle de glissette. On peut aussi obtenir physiquement une conchoïde par anamorphose cylindrique.

Cette notion est aussi un cas particulier de celle de cissoïdale qui peut être considérée comme une conchoïde de module variable.

La conchoïde de module a est souvent égale à celle de module –a , et l'on peut désigner par conchoïde complète la réunion de ces deux conchoïdes. Cette conchoïde complète est alors le lieu des points d'intersection d'un cercle de rayon a centré en M₀ avec la droite (OM₀).

Exemples :
    - les conchoïdes de droite, ou conchoïdes de Nicomède.
    - les conchoïdes de cercle, dont les limaçons de Pascal quand le pôle est sur le cercle.
    - les conchoïdes de conique par rapport au foyer, dont les courbes de Jerabek.
    - les conchoïdes de rosaces.
    - les conchoïdes de strophoïde droite par rapport au sommet de la boucle sont les strophoïdes.
    - les conchoïdes de spirale d’Archimède par rapport au centre sont des spirales d’Archimède isométriques.

Les conchoïdes de Dürer sont d'un autre type.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2022