Du grec Kogkhoeidês : semblable à une coquille (cf. la conchyliculture : élevage des coquillages).

 

Pour un cercle de centre O et de rayon b = ka, un pôle de conchoïde en A(a, 0) et un module égal à c = la : Paramétrisation cartésienne : . Équation cartésienne (correspondant à la réunion des deux courbes pour l et –l ): . Sextique. Équation polaire dans le repère de centre A : .

 

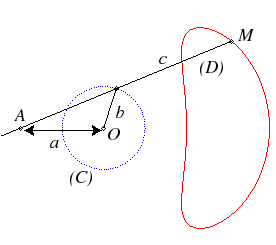
Les conchoïdes de cercle peuvent être vues comme les trajectoires des points d'une bielle (D) astreinte à coulisser par un point fixe (le pôle, ici A) et dont un point X décrit un cercle (C)  (ici de centre O et de rayon b, le point traceur M étant à une distance (signée) c de X. Le mécanisme associé est dit "de Wittgenstein".

Lorsque le pôle est sur le cercle, on obtient les limaçons de Pascal.
 
 

Tracé animé dans le cas où le pôle est extérieur au cercle (k < 1) ; comme on le remarque, certaines portions sont quasi rectilignes, ce qui a été utilisé en pratique : il s'agit du mécanisme de Hoecken (cf. aussi la courbe de Watt).
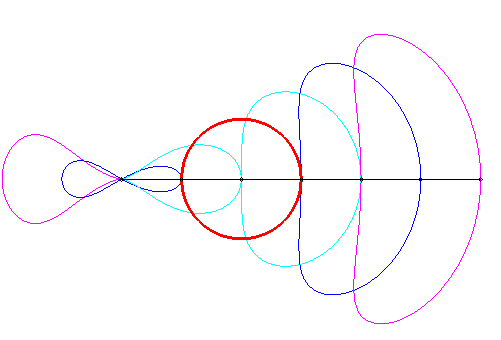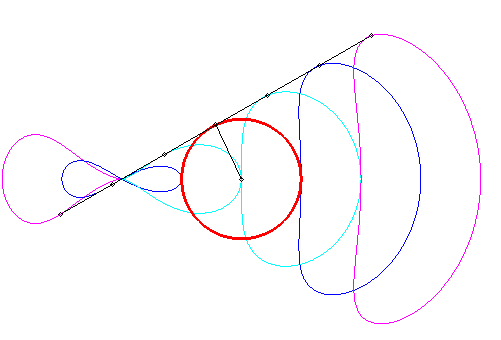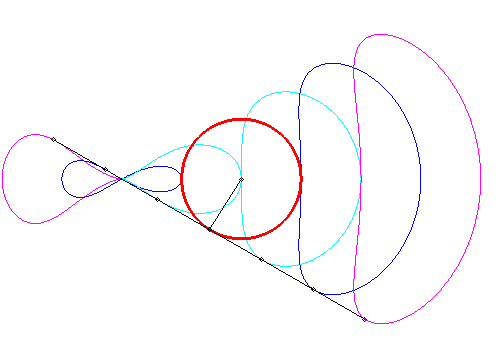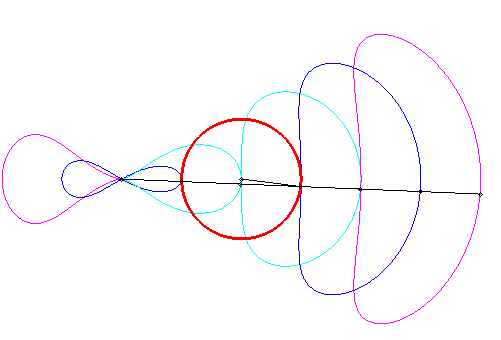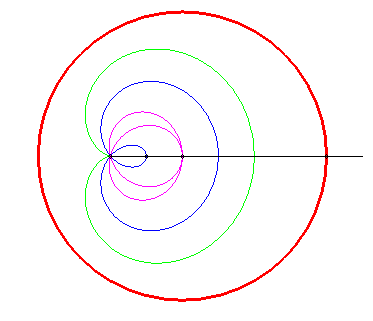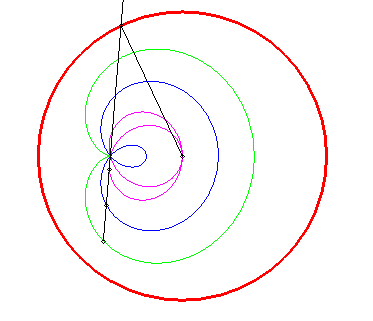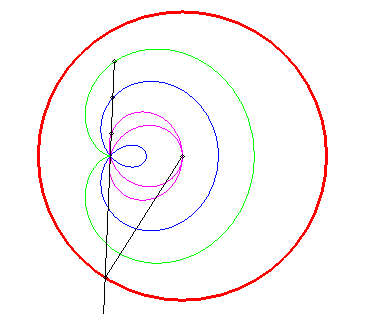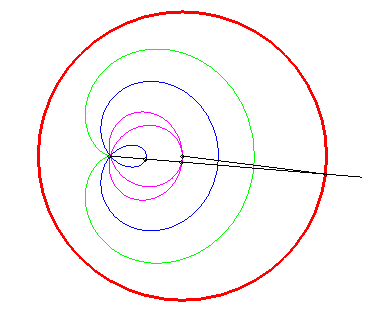
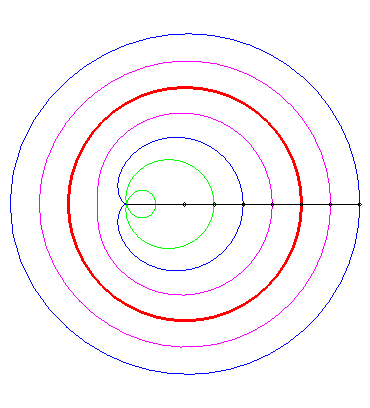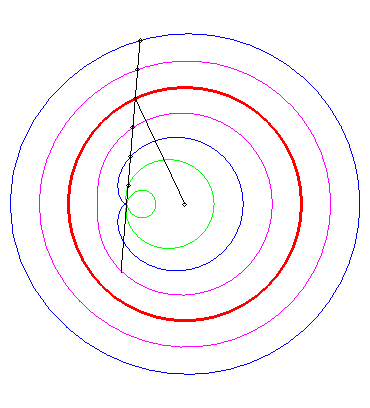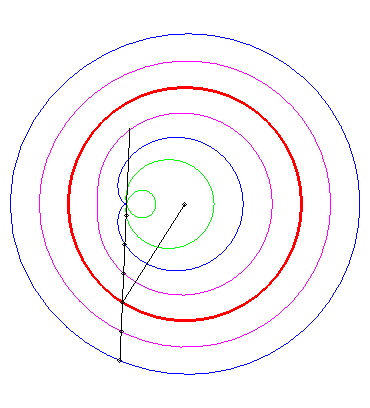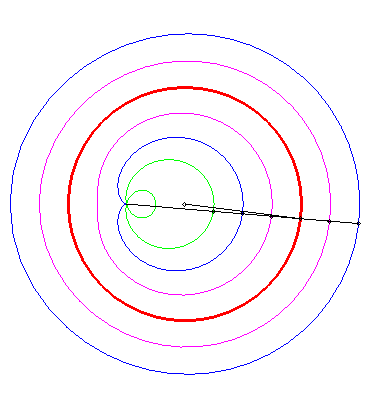
Tracé animé dans le cas où le pôle est intérieur au cercle (k > 1).

 

On peut s'intéresser plus généralement au mouvement plan sur plan dit conchoïdal circulaire (étudié plus précisément ici),  le plan mobile étant le plan lié à la droite (), décrivant le cercle (C) (et  étant fixe dans le plan mobile) : en effet, les conchoïdes de cercle sont les roulettes de ce mouvement, pour des points traceurs situés sur la droite (D). La base (en mauve ci-contre) de ce mouvement est la courbe d'équation polaire  qui n'est autre que la courbe de Jerabek et la roulante (en turquoise) la courbe de paramétrisation cartésienne : , étudiée sur cette page.

 

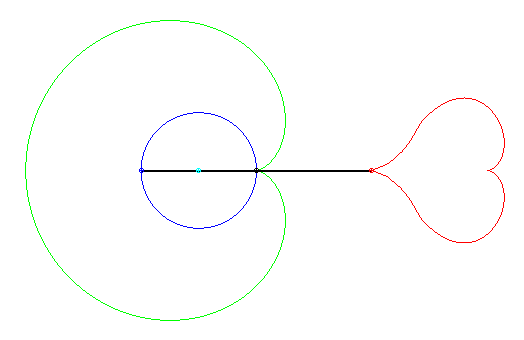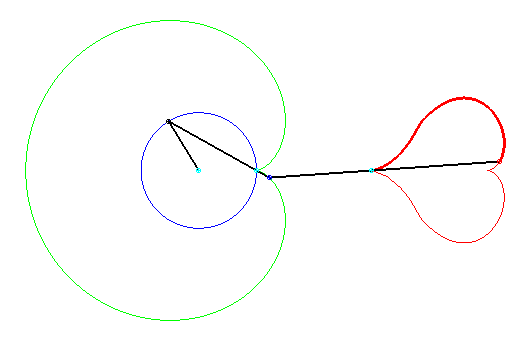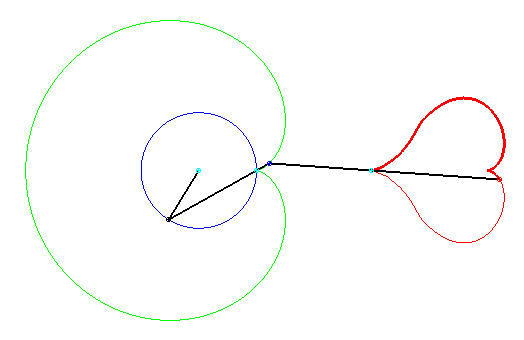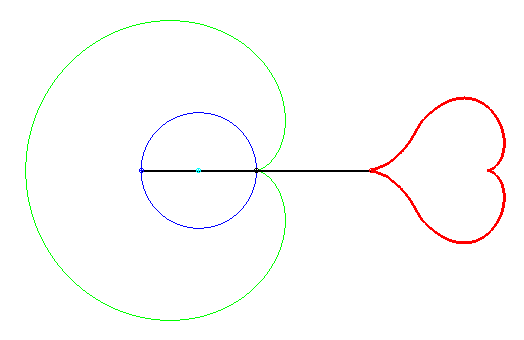
Les conchoïdes de conchoïdes de cercle prennent des formes variées, dont ce joli coeur.  Si le cercle de départ est de rayon a, la première barre est de longueur 2a, la deuxième barre de longueur 4a, le premier pôle est sur le cercle, et le deuxième pôle à une distance 2a du premier. La première conchoïde est une cardioïde. Coeur découvert par Keishiro Ueki.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2023