BASE DU SYSTEME BIELLE-MANIVELLE
Base
of the slider-crank mechanism

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BASE DU SYSTEME BIELLE-MANIVELLE
Base
of the slider-crank mechanism

| Nom maison. |
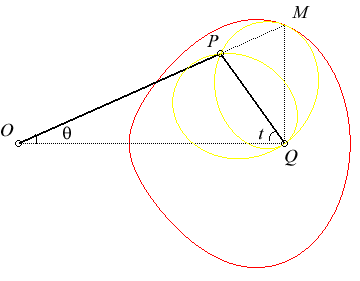 |
Si la manivelle OP = a et la bielle
PQ
= b :
Équation polaire : Paramétrisation cartésienne : 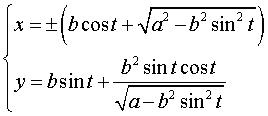
( Équation cartésienne : Sextique de genre 1. |
| Étant donné un mécanisme articulé
(OPQ), O étant fixe et Q astreint à
se mouvoir sur une droite (D) passant par O (ici : Ox), la
courbe (G) qui nous occupe est le lieu
du point de la droite (OP) qui se projette sur (D) en Q.
C'est donc la base du mouvement
du plan dont P est un point fixe, et (PQ) une droite fixe,
mouvement dit du système bielle manivelle,
(d'où le nom donné à cette courbe) ; la roulante du
mouvement (en jaune ci-contre) est la courbe
de Jerabek.
|
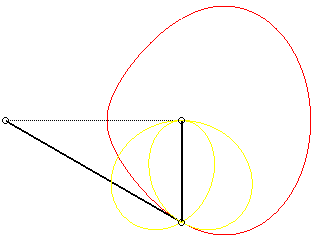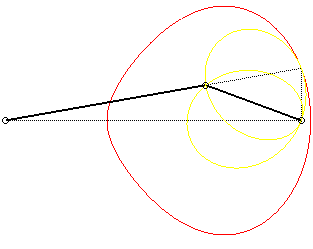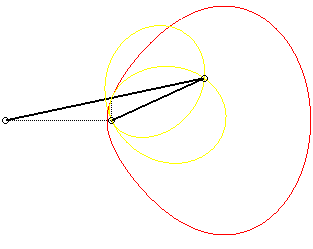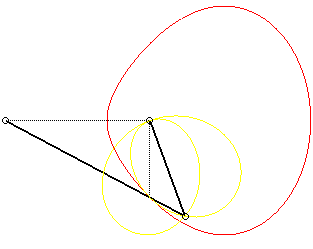 |
La courbe possède deux composantes bornées
lorsque la manivelle est supérieure à la bielle (a >
b)
, et deux composantes à asymptotes quand (a < b) ; pour
a
= b, c'est un cercle.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2007