next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

BASE OF THE SLIDER-CRANK MECHANISM

Self-invented name.

 
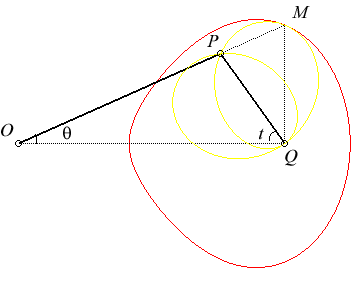Let OP = a be the crank and PQ = b be the connecting rod:
Polar equation: .
Cartesian parametrization: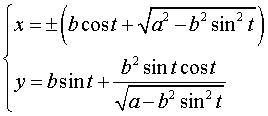 
().
Cartesian equation: .
Sextic of genus 1.

 
Given an articulated mechanism (OPQ), O being fixed and Q being bound to move on a straight line D passing through O (here Ox), the curve (G) that we are studying is the locus of the points of the line (OP) whose projection on D is Q.

Therefore, it is the base of the movement of the plane for which P is a fixed point and (PQ) a fixed line. This movement is called the slider-crank mechanism, (hence the name of this curve). The rolling curve of the movement (in yellow on the figure on the right) is Jerabek's curve.
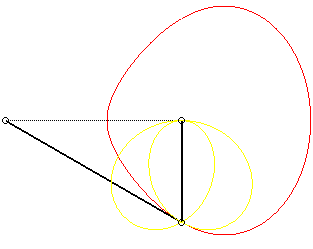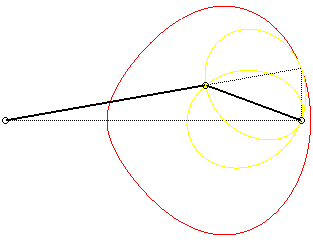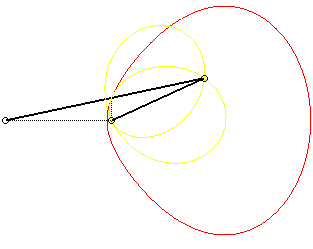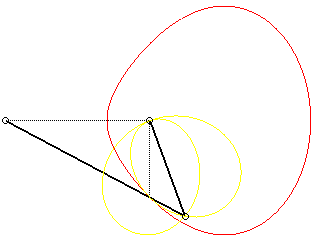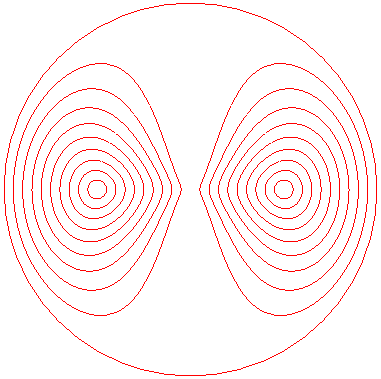
(G) is thus also the rolling curve of the movement of the circular conchoidal mechanism, which is dual to the former mechanism.    . 

The curve has two bounded components when the crank is longer than the connecting rod (a > b), and two components with asymptotes when a < b; when a = b, it is a circle.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2017