Cartesian parametrization:
Cartesian equation (corresponding to the reunion of the two curves for l and –l):
Sextic.
Polar equation in the frame centred on A:
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
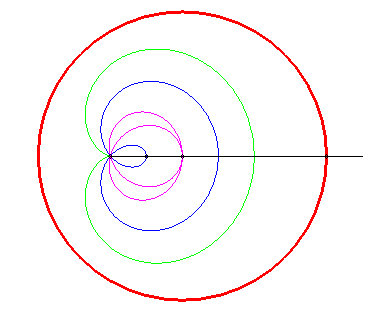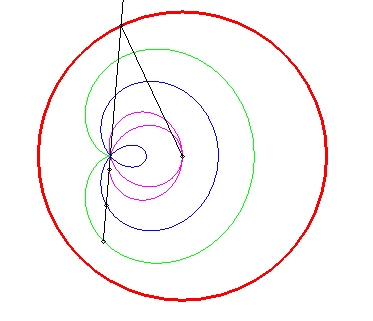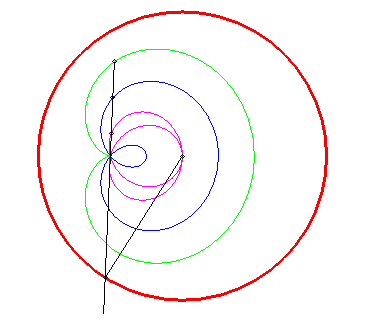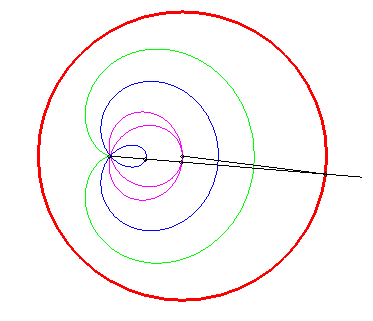
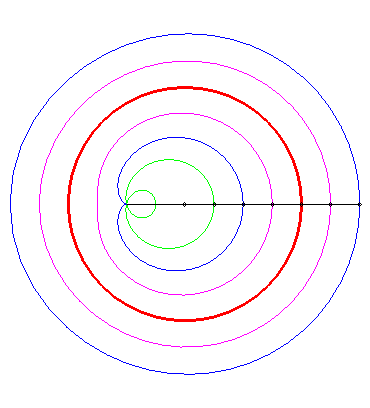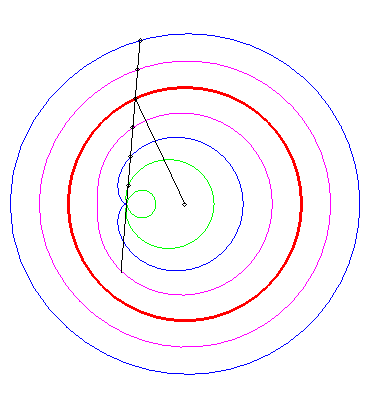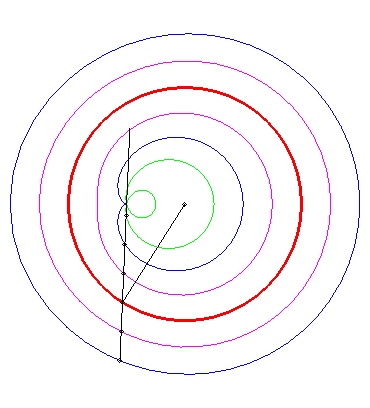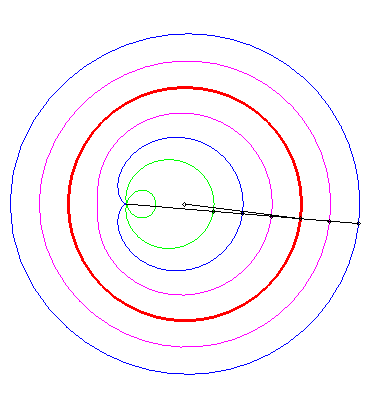
CONCHOID OF A CIRCLE
| From the Greek Kogkhoeidês: similar to a shell. |
| For a circle with centre O and radius b =
ka,
the pole of the conchoid being A(a, 0) and the modulus c
= la:
Cartesian parametrization: Cartesian equation (corresponding to the reunion of the two curves for l and –l): Sextic. Polar equation in the frame centred on A: |
| The conchoids of circles can be seen as the trajectories of the points on a connecting rod (D) constrained to slide through a fixed point (the pole, here A) and one of the points of which describes a circles (C) (here with centre O and radius b). | 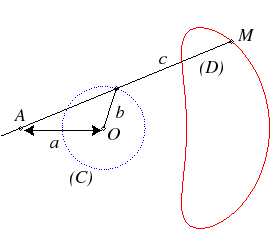 |
When the pole is on the circle, we get the limaçons
of Pascal.
| Animated drawing in the case where the pole is outside the circle (k < 1); as it can be noticed, certain portions are almost linear, which is used in practice : it's the Hoecken's linkage (see also Watt's curve). |
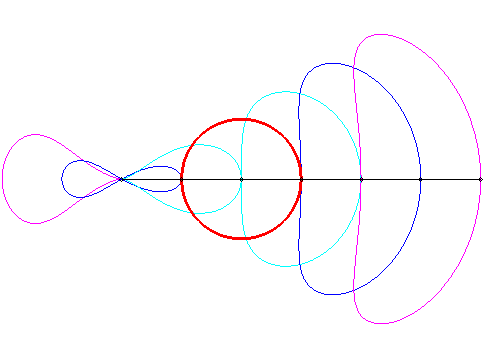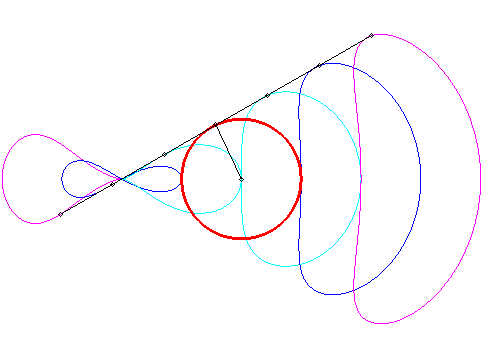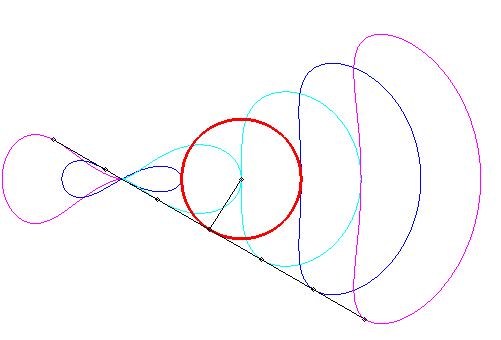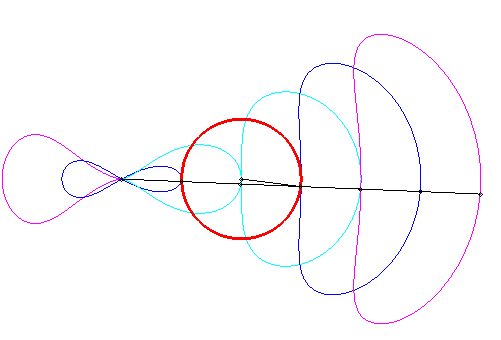 |
|
Animated drawing in the case where the pole is inside the circle (k > 1). |
  |
| One can also take an interest, more generally, to the
movement
of a plane over a fixed plane called circular conchoidal motion
(studied more precisely here),
the moving plane being the one linked to the line ( The base (in mauve opposite) of this movement is
the curve with polar equation |
 |
|
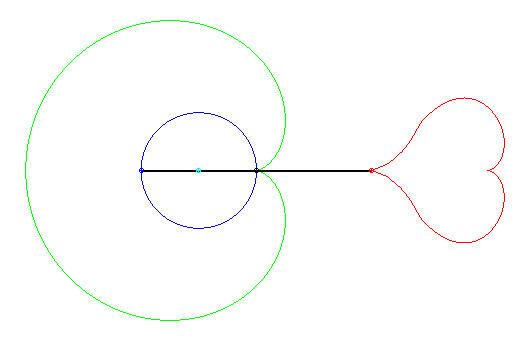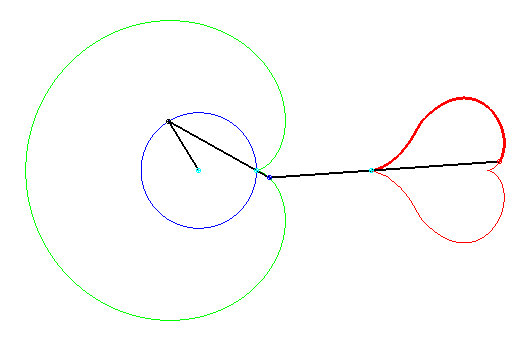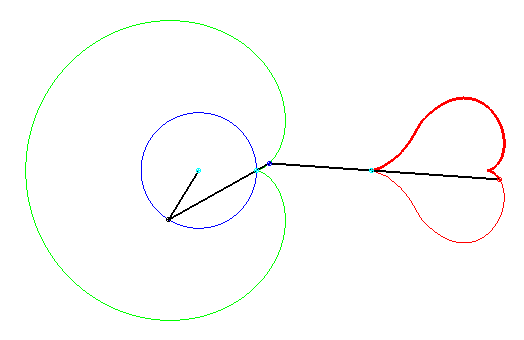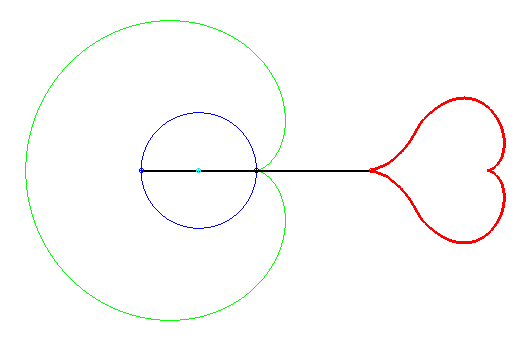
Circle conchoid conchoids come in a variety of shapes, including this cute heart. If the starting circle has radius a, the first bar has length 2a, the second bar has length 4a, the first pole is on the circle, and the second pole at a distance 2a from the first. Heart discovered by Keishiro Ueki. |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2023