Movement of a plane over a fixed plane

EXAMPLES OF MOVEMENTS OF A PLANE OVER A FIXED PLANE

The following examples are special cases of the movements obtained by slipping, studied on this page.

EXAMPLE 1

Movement of a circular conchoidal slider-crank mechanism.
Movement of a plane carried by a connecting rod that passes by a fixed point and that has one of its ends in a circular movement. Movement of the classic slider-crank mechanism.
Movement of a plane carried by a connecting rod that has one of its ends in a circular movement while the other has a linear movement (on a straight line passing by the centre of the circle)

The base (in mauve) is the locus of the instant centre of rotation in the fixed plane, and the rolling curve (in turquoise) is the locus of this centre in the moving plane.
It can be noted in the examples above that the bases and rolling curves are exchanged. How can this be explained?

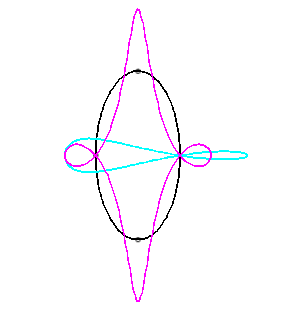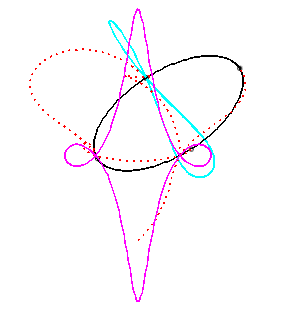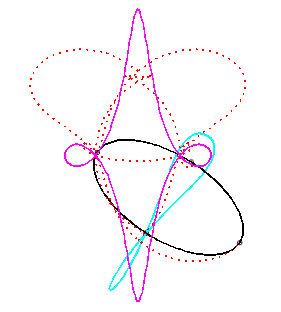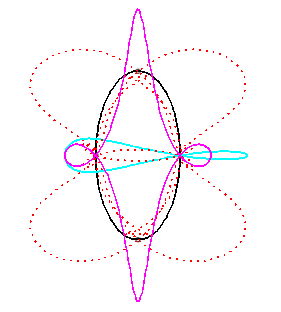
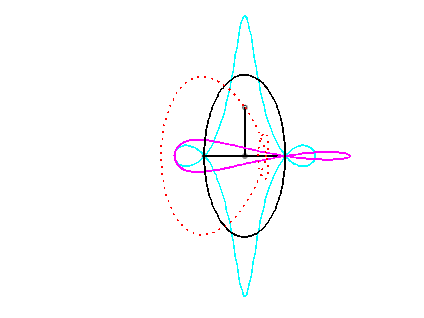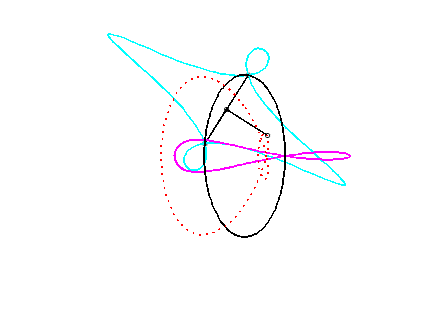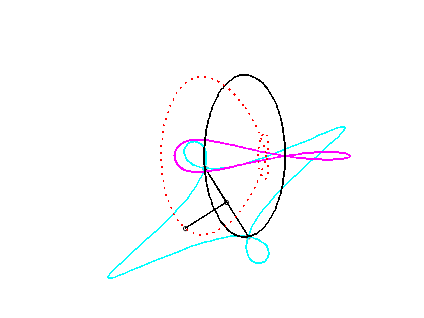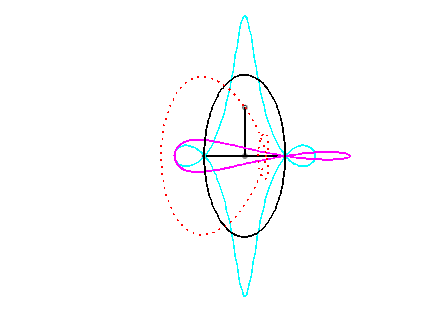
For an observer located on the connecting rod [PQ], the point O has a circular movement around P; the distance AO being constant, for him, the segment [AO] is a connecting rod whose extremity A has a linear movement along [PQ] while the other extremity O has a circular movement carried by the crank [PO]. Therefore, the relative motion of the moving plane with respect to the fixed plane is the one studied in the column on the right, hence the exchange of the bases and the rolling curves.
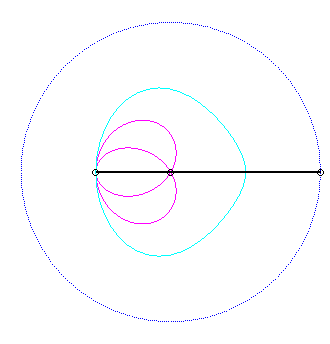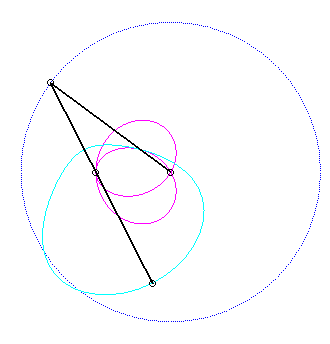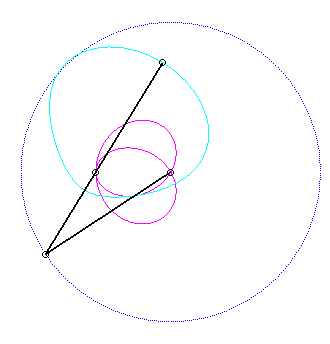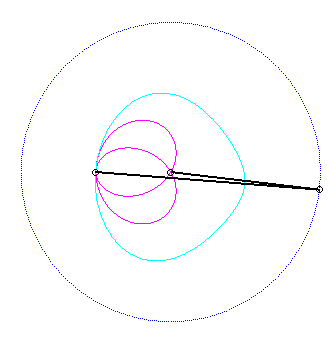
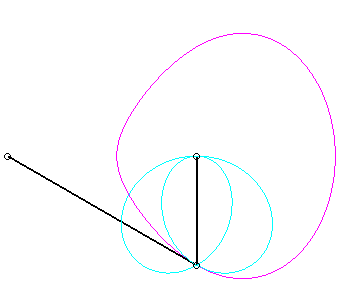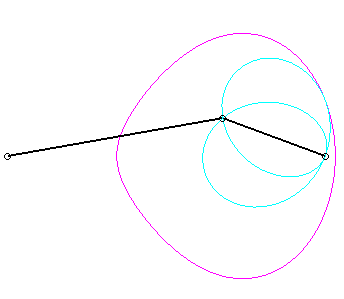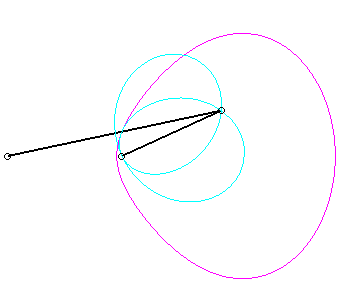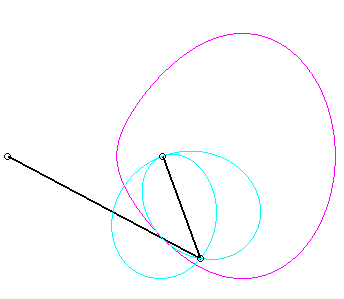
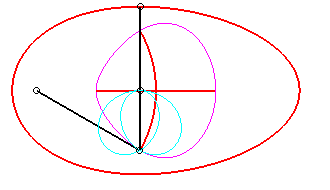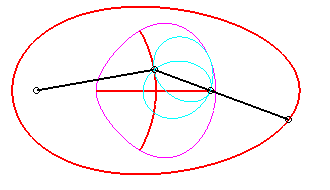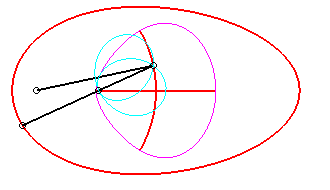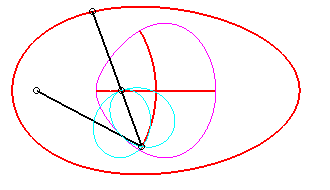
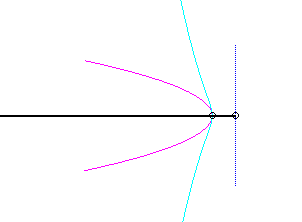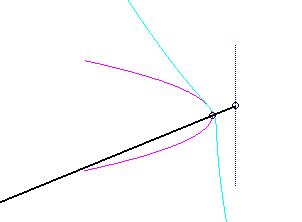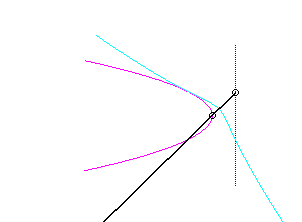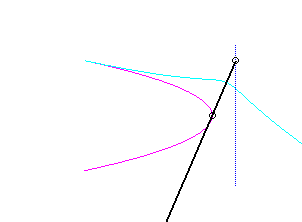
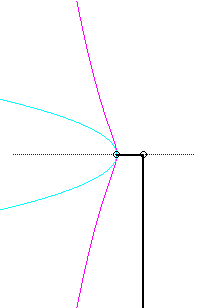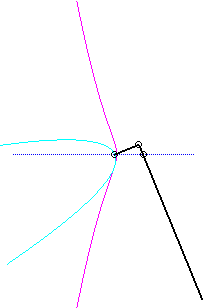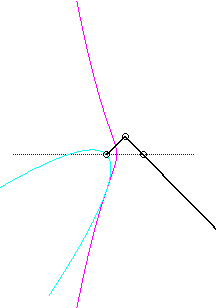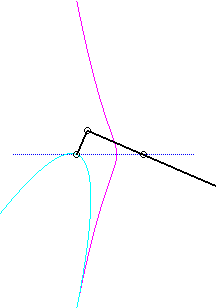
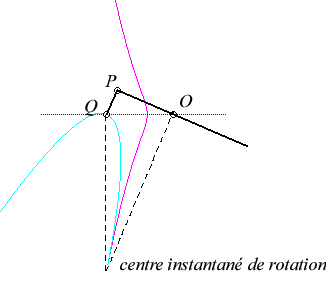
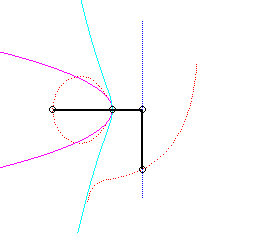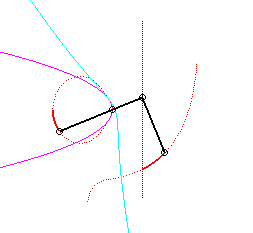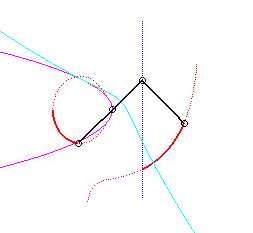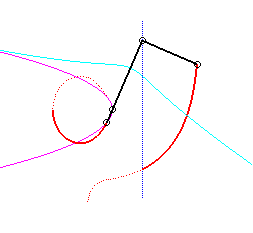
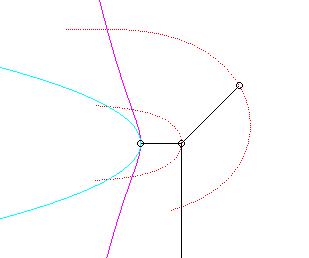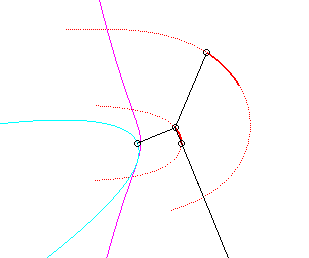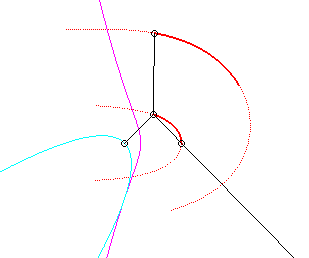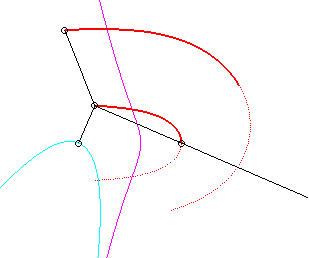
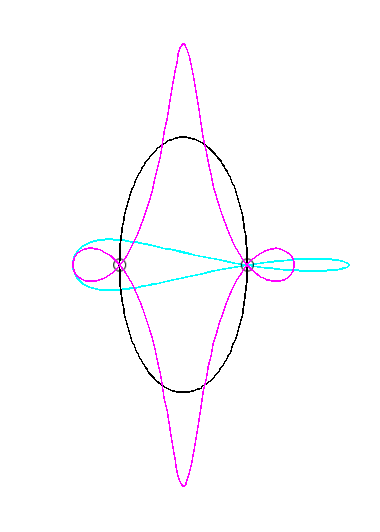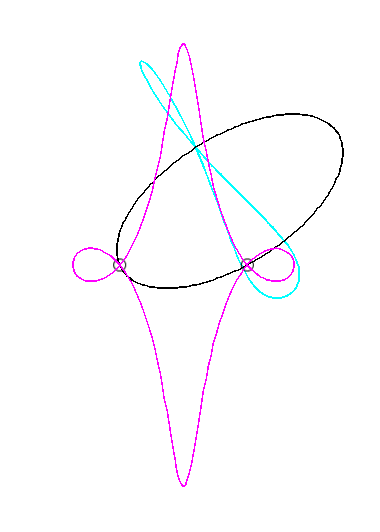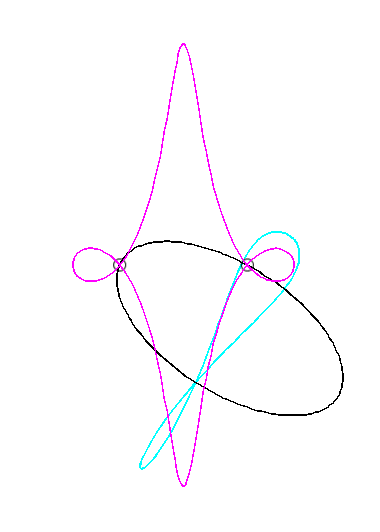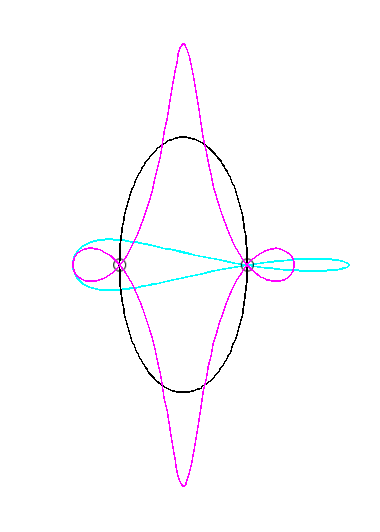
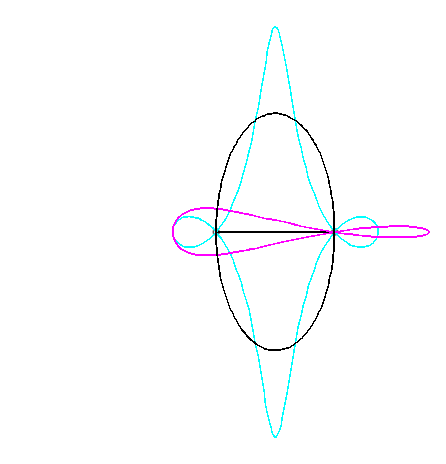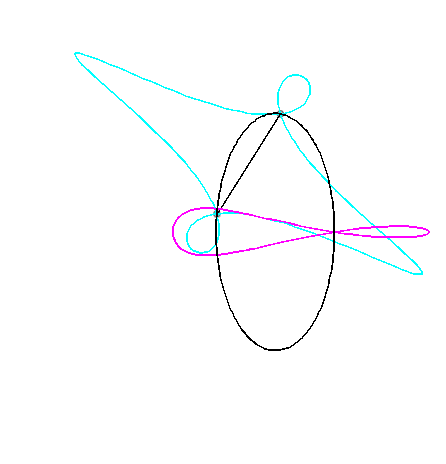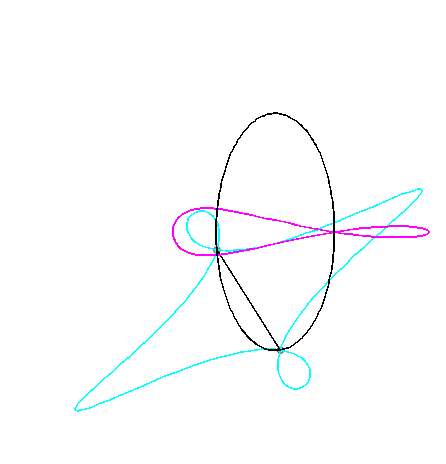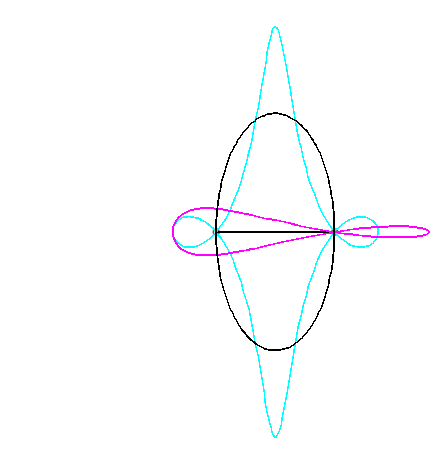
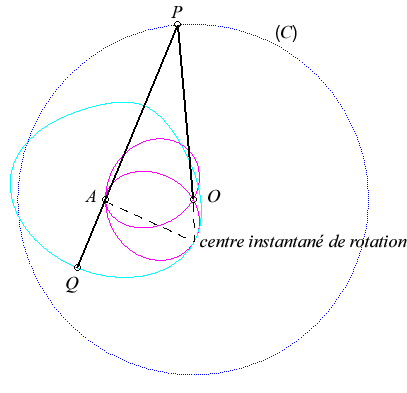
Since the velocity vector of A (seen as a point in the moving plane) lies on (PA) and P's one is tangent to (C), the instant centre of rotation M is at the intersection of the perpendicular to (PQ) passing through A and the line (OP).
The base, the locus of M in the fixed plane, is thus, by definition, Jerabek's curve.

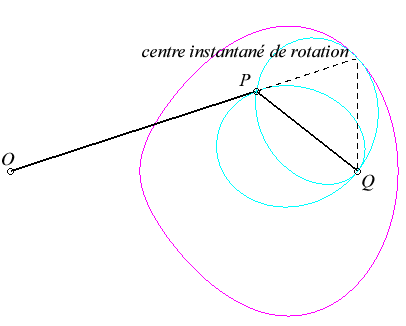
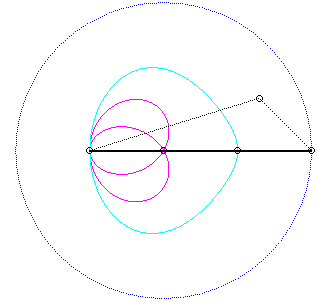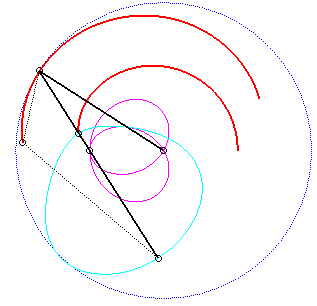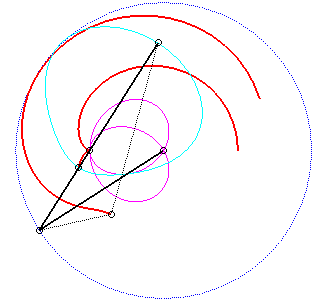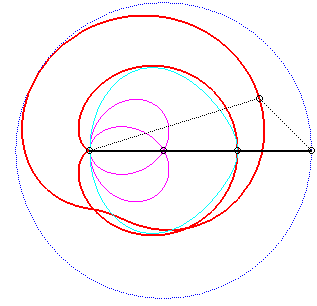
For an observer located on the connecting rod [PQ], the point O has a circular movement around P; for him, the line (OQ) is a connecting rod whose extremity O has a circular movement and that is sliding while passing through the fixed point Q. Therefore, the relative movement of the moving plane with respect to the fixed plane is the one studied in the column on the left, hence the exchange of the bases and the rolling curves.
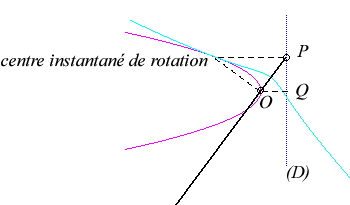
Since the velocity vector of Q (seen as a point in the moving plane) lies on (OQ) and P's one is perpendicular to [OP], the instant centre of rotation M is at the intersection of the perpendicular to (OQ) passing through Q and the line (OP).
Since the base, the locus of M in the fixed plane, has not, to my knowledge, been given a name, I named it "base of the slider-crank mechanism".

These movements are said to be dual, or inverse of one another

Animated drawing of two roulettes (trajectories, in the fixed plane, of points fixed in the moving plane).
The points on the line containing the connecting rod trace conchoids of the blue circle; the other points trace isocondoids; see conchoids of a circle.

Animated drawing of 3 roulettes, including the circular and the linear ones.
The roulettes are curves of the slider-crank mechanism.

EXAMPLE 2

Linear conchoidal movement.
Movement of a plane carried by a rod having an extremity in a linear motion and passing through a fixed point. Movement of the set square, or "of the kappa".
Movement of a plane carried by a set square with one side sliding through a point O and with a point on the other side describing a line passing by O.

Note that, again, the bases and the rolling curves are exchanged; do you have an explanation?

For an observer located on the rod [PO], the extremity O of the right angle (OQP) has a linear movement along (OP) and its side [QP) slides through the point P (that is fixed for the observer). Therefore, the relative motion of the moving plane with respect to the fixed plane is the one studied in the column on the right, hence the exchange of the bases and the rolling curves.
Since the velocity vector of O (seen as a point in the moving plane) lies on (PO) and P's one lies on (D), the instant centre of rotation M is at the intersection of the perpendicular line to (PO) passing through O and the perpendicular line to (D) passing through P.

We can prove that the base, the locus of M in the fixed plane, is a parabola (whose focus F satisfies ).
For an observer located on the rod [PQ], the point O has a linear movement (along the line (OP) that does not move, for him) and carries with him the rod (OQ) that slides in Q. Therefore, the relative motion of the moving plane with respect to the fixed plane is the one studied in the column on the left, hence the exchange of the bases and the rolling curves.
Since the velocity vector of Q (seen as a point in the moving plane) lies on (OQ) and O's one is perpendicular to [OP], the instant centre of rotation M is at the intersection of the perpendicular to (OQ) passing through Q and the perpendicular to (OP) passing through O.
We can prove the the base, the locus of M in the fixed plane, is a Kampyle of Eudoxus.

Animated drawing of two roulettes.
The points on the straight line trace conchoids of the blue line; the other points trace isoconchoids; see conchoid of Nicomedes.
Animated drawing of two roulettes.
The vertex of the set square describes a kappa. Therefore, the points of the sliding lines trace conchoids of kappa, and the other points isoconchoids.
Compare with Newton's set square (similar mechanism, but the line described by the point Q does not pass by O), whose roulettes are the right circular rational cubics.

EXAMPLE 3

Movement of a plane tied to an ellipse passing by two fixed points.
Case where the length of the minor axis equals the distance between the two points. Movement of a plane tied to a rod whose extremities slide on an ellipse, dual to the previous one. Case where the length of the minor axis equals the length of the rod.

Same animation with the drawing of the roulettes of the 4 vertices of the ellipse. Same animation with the drawing of a roulette.

Parametrization of the base above:; see also this page by Alain Esculier.

Movement of a circular conchoidal slider-crank mechanism. Movement of a plane carried by a connecting rod that passes by a fixed point and that has one of its ends in a circular movement.	Movement of the classic slider-crank mechanism. Movement of a plane carried by a connecting rod that has one of its ends in a circular movement while the other has a linear movement (on a straight line passing by the centre of the circle)

Linear conchoidal movement. Movement of a plane carried by a rod having an extremity in a linear motion and passing through a fixed point.	Movement of the set square, or "of the kappa". Movement of a plane carried by a set square with one side sliding through a point O and with a point on the other side describing a line passing by O.

Movement of a plane tied to an ellipse passing by two fixed points. Case where the length of the minor axis equals the distance between the two points.	Movement of a plane tied to a rod whose extremities slide on an ellipse, dual to the previous one. Case where the length of the minor axis equals the length of the rod.

Same animation with the drawing of the roulettes of the 4 vertices of the ellipse.	Same animation with the drawing of a roulette.