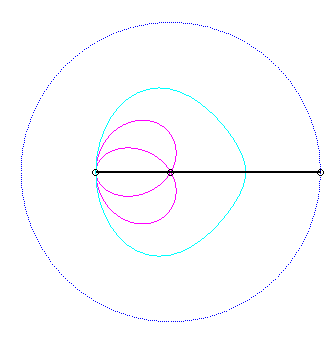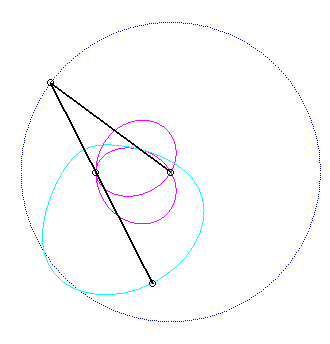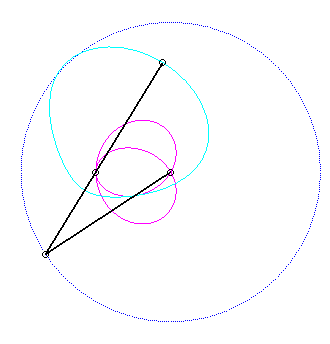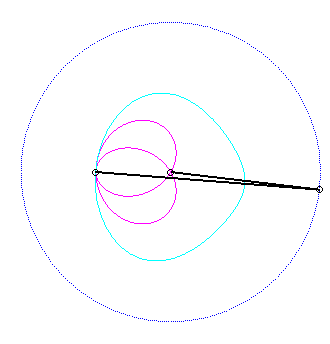
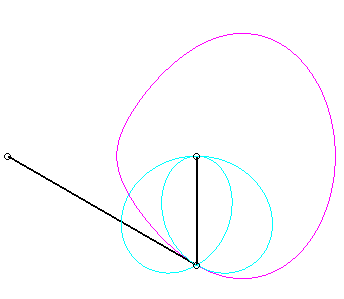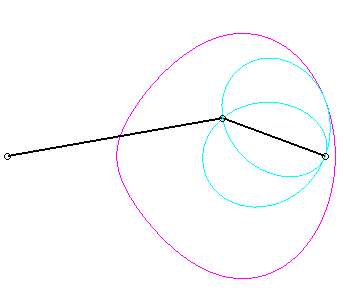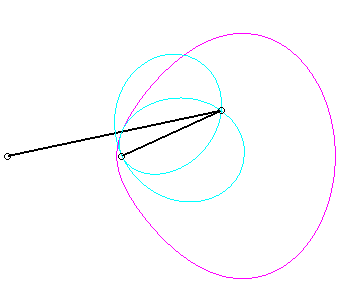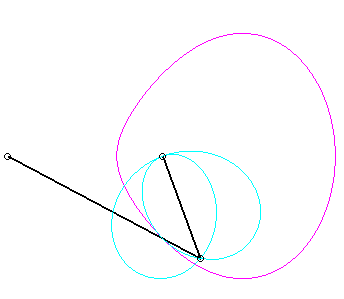
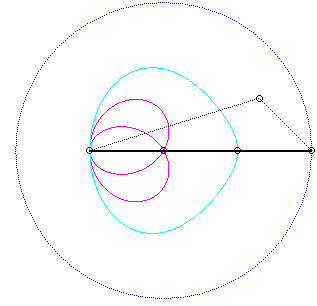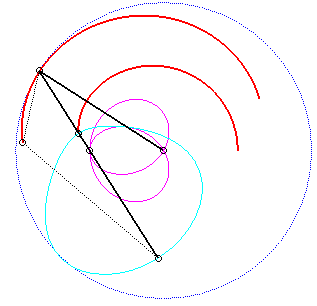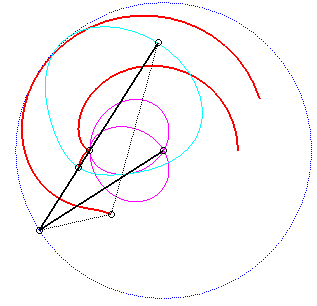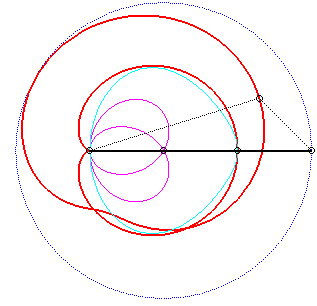
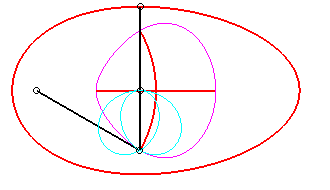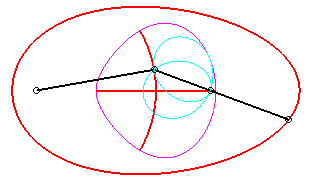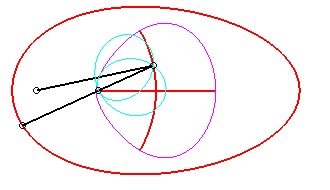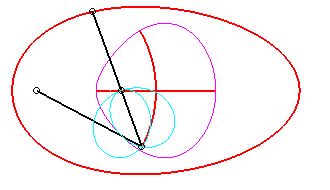
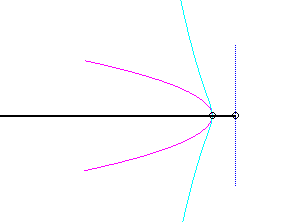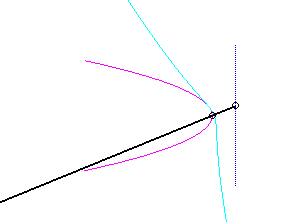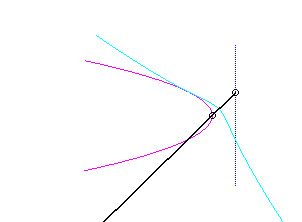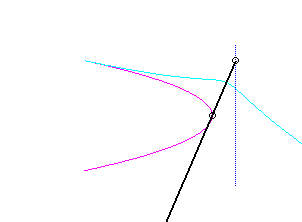
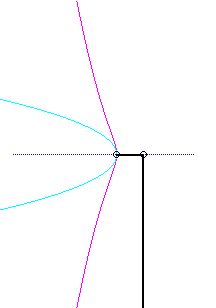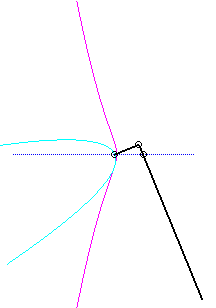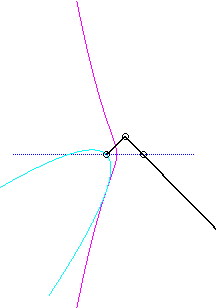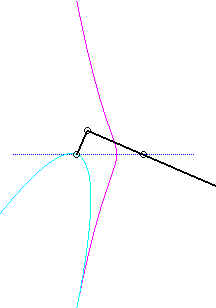
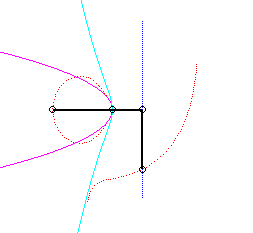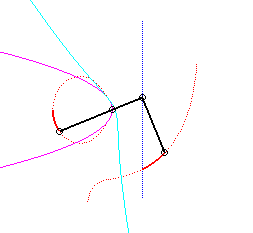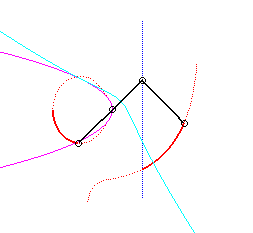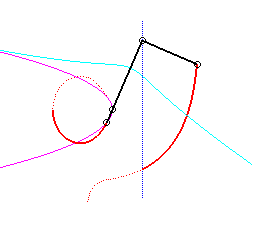
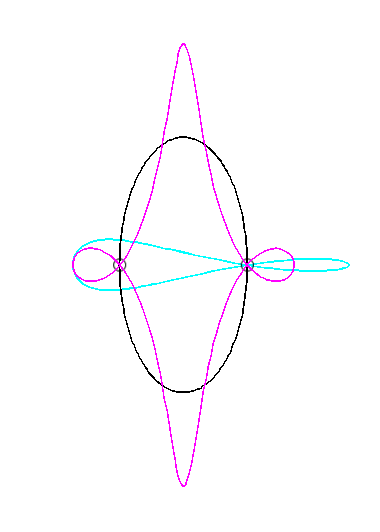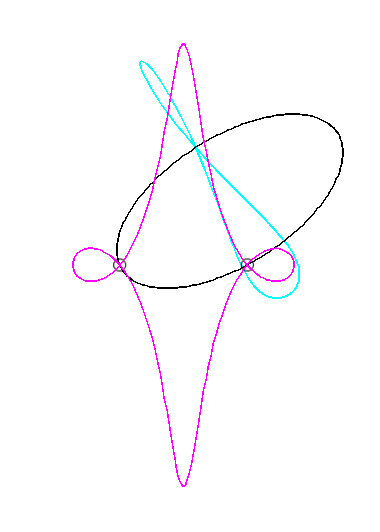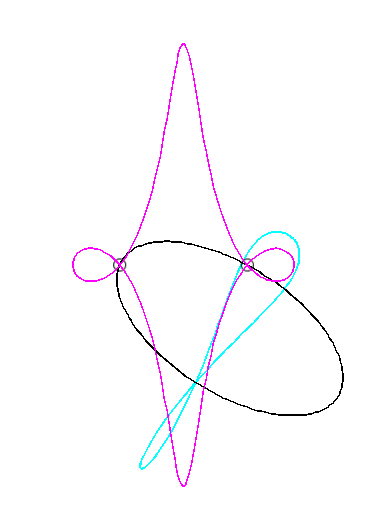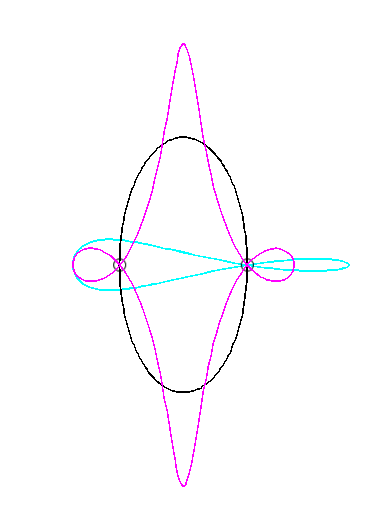
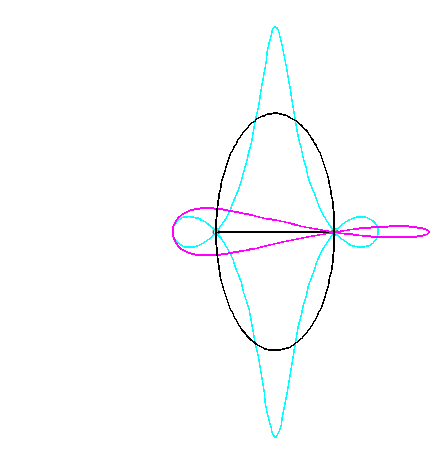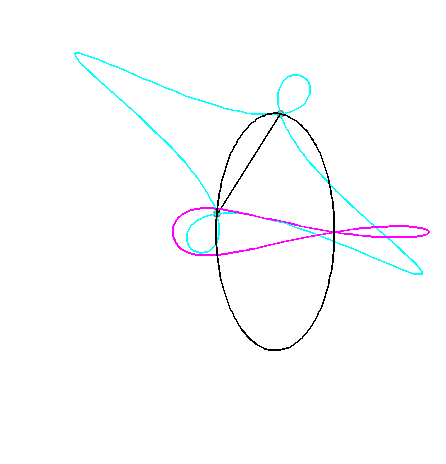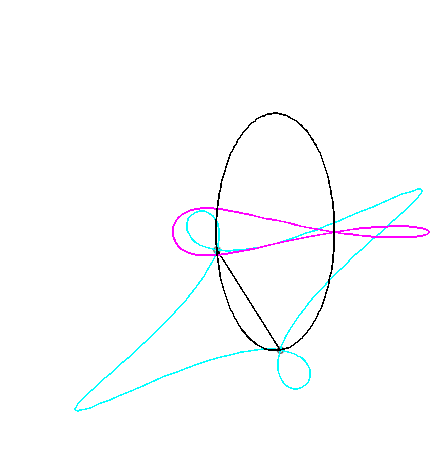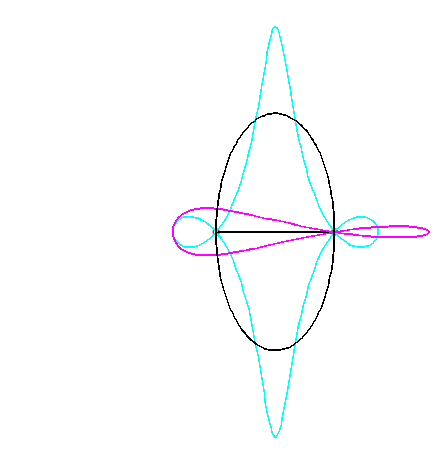
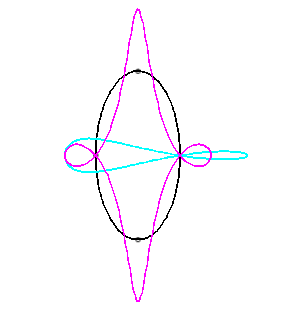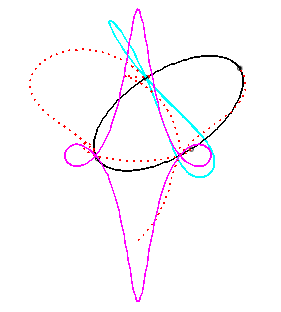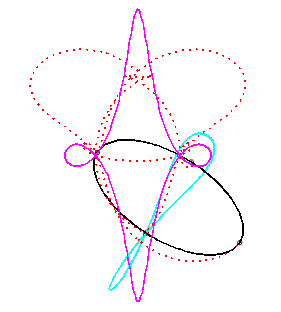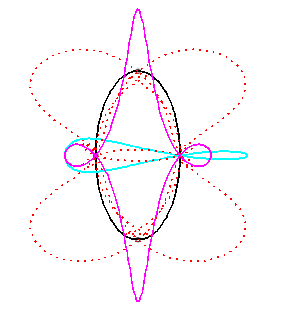
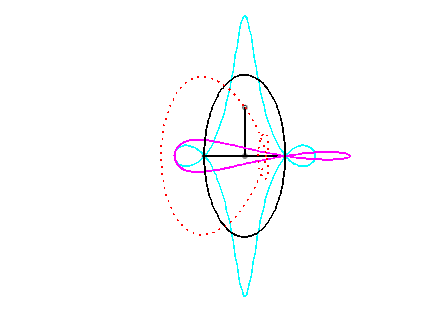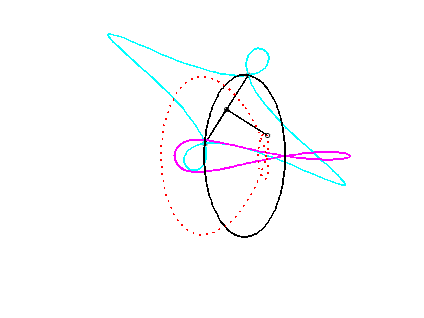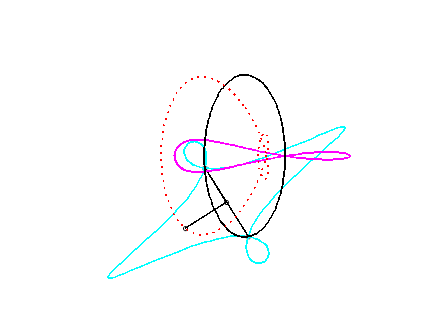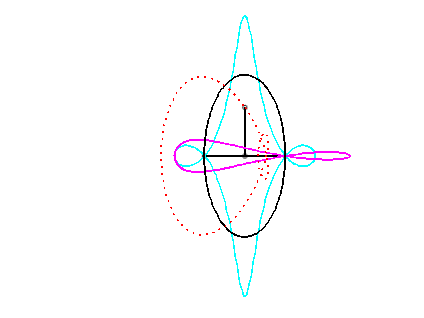
 Pour un observateur placé sur la bielle [PQ],
le point O a un mouvement circulaire autour de P ;
la distance AO étant constante, pour lui, le segment [AO]
est une bielle dont l'extrémité A a un mouvement rectiligne
le long de [PQ] et l'autre extrémité O un mouvement
circulaire entraîné par la manivelle [PO]. Le mouvement
relatif du plan mobile par rapport au plan fixe est donc celui étudié
dans la colonne de droite, d'où l'explication de l'échange
des bases et roulantes.
Pour un observateur placé sur la bielle [PQ],
le point O a un mouvement circulaire autour de P ;
la distance AO étant constante, pour lui, le segment [AO]
est une bielle dont l'extrémité A a un mouvement rectiligne
le long de [PQ] et l'autre extrémité O un mouvement
circulaire entraîné par la manivelle [PO]. Le mouvement
relatif du plan mobile par rapport au plan fixe est donc celui étudié
dans la colonne de droite, d'où l'explication de l'échange
des bases et roulantes.
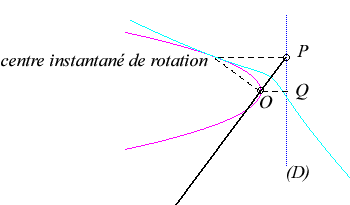
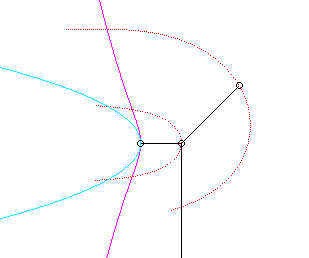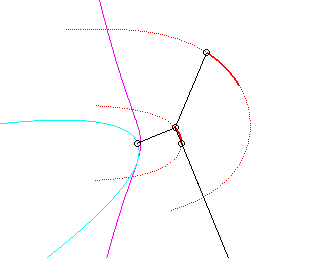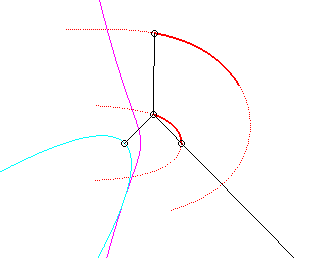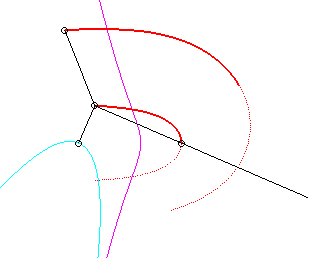
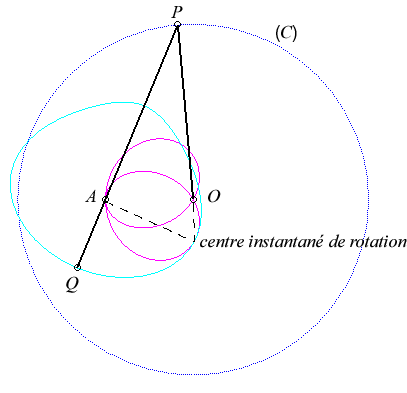
Le vecteur vitesse de A (considéré
comme point du plan mobile) étant porté par (PA),
et celui de P étant tangent à (C), le centre
instantané de rotation M est à l'intersection de la
perpendiculaire à (PQ) passant par A et de la droite
(OP).
La base, lieu de M dans
le plan fixe, est donc par définition la courbe
de Jerabek. |
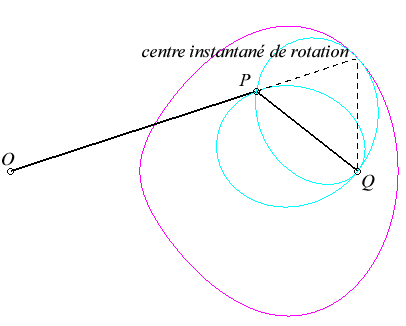
Pour un observateur placé sur la bielle [PQ],
le point O a un mouvement circulaire autour de P ; pour lui,
la droite (OQ) est une bielle dont l'extrémité
O
a
un mouvement circulaire et coulissant par le point fixe Q. Le mouvement
relatif du plan mobile par rapport au plan fixe est donc celui étudié
dans la colonne de gauche, d'où l'explication de l'échange
des bases et roulantes.
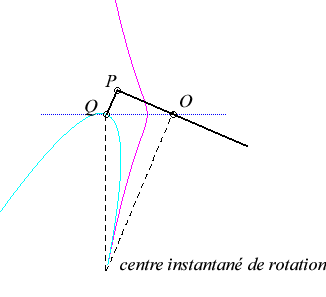
Le vecteur vitesse de Q (considéré
comme point du plan mobile) étant porté par (OQ),
et celui de P étant perpendiculaire à [OP],
le centre instantané de rotation M est à l'intersection
de la perpendiculaire à (OQ) passant par Q et de la
droite (OP).
La base, lieu de M dans
le plan fixe, n'ayant pas à ma connaissance
reçu de nom, je l'ai nommée "base
du système bielle-manivelle".
|