Pour une conique d'excentricité e et de paramètre a, et une conchoïde de module ka : Équation polaire :  (forme générale : ). Équation cartésienne : . Quartique rationnelle.

Les conchoïdes focales de conique sont les conchoïdes de conique par rapport à un des foyers de la conique.
 

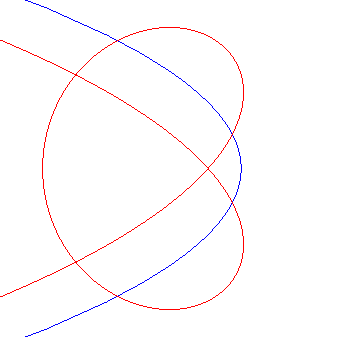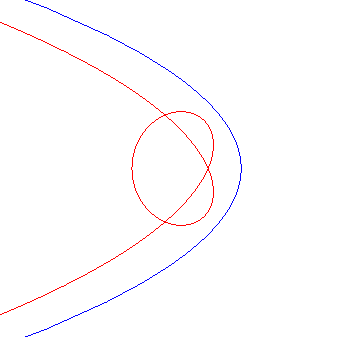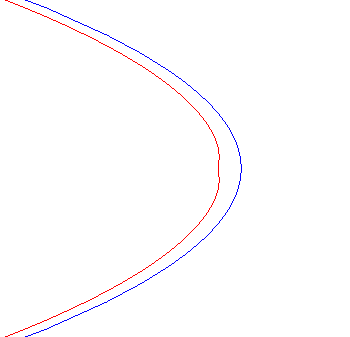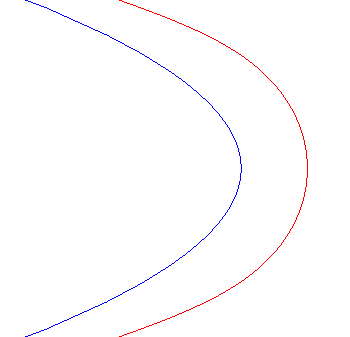
Cas d'une ellipse
Cas d'une parabole
Cas d'une hyperbole

 
 

Lorsque  (c'est à dire quand le module ka de la conchoïde est l'opposé du demi-grand axe pour une ellipse, ou le demi-axe focal pour une hyperbole), on obtient les courbes de Jerabek.
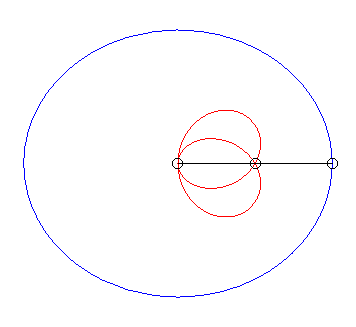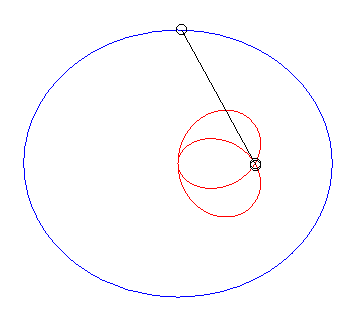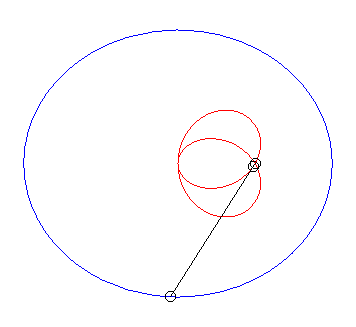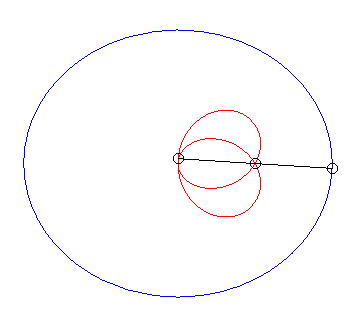Lorsque k = –1 (c'est à dire quand le module de la conchoïde est l'opposé du paramètre de la conique) on obtient des courbes à point double à tangentes confondues :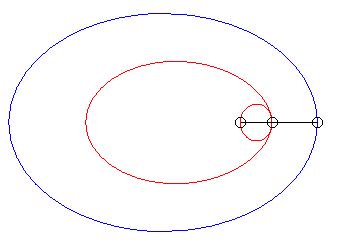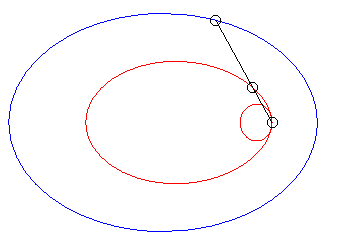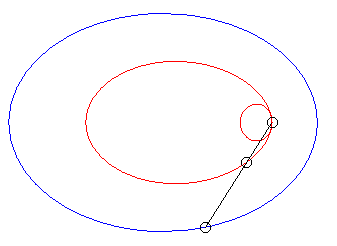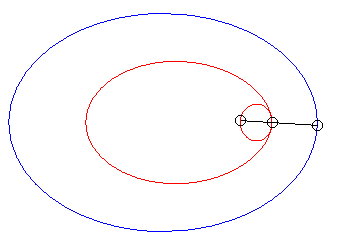
Lorsque  (c'est à dire quand le module de la conchoïde est l'opposé de la distance du foyer au sommet) on obtient des courbes à point de rebroussement :

 
 

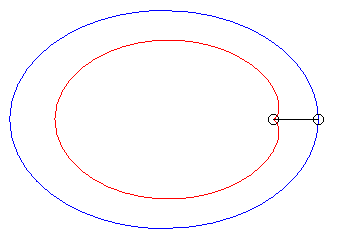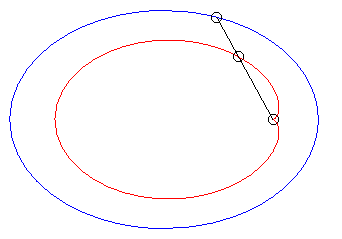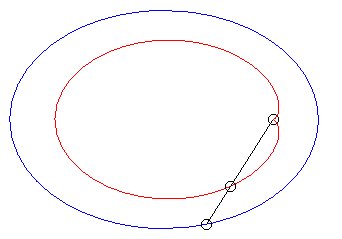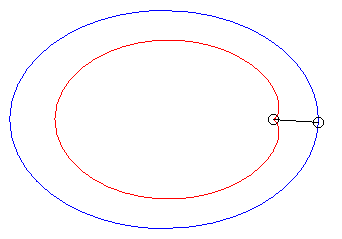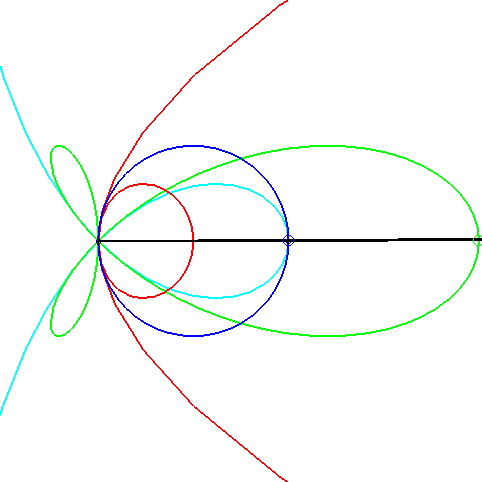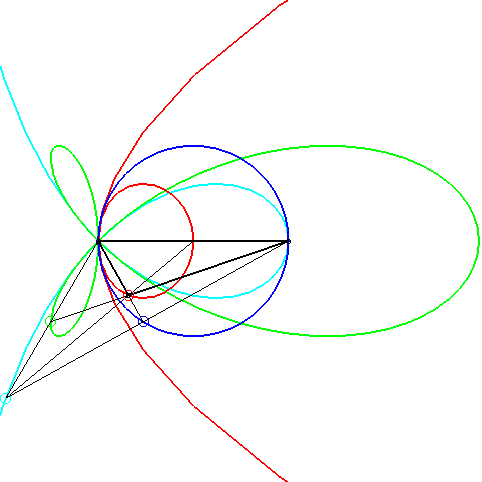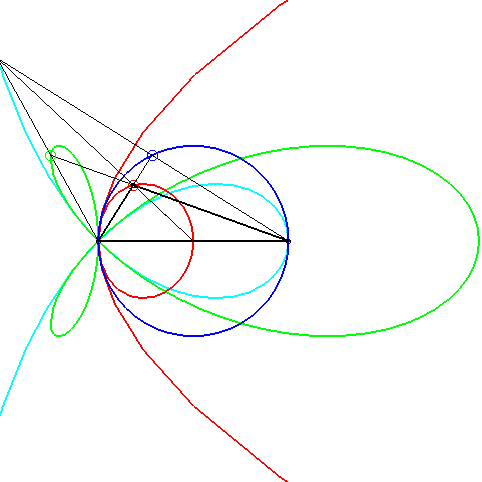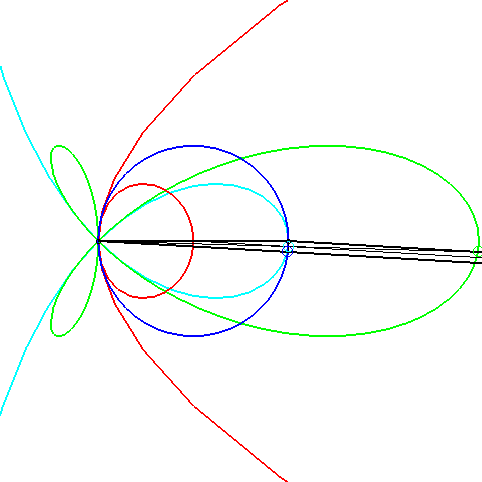
Une conchoïde de parabole avec k = –1 intervient dans le problème de la détermination des triangles tels que la médiane issue d'un sommet, la hauteur issue d'un autre, et l'une des bissectrices issue du dernier concourent. Lorsque l'on fixe le côté croisant la médiane, le sommet opposé d'un tel triangle décrit une conchoïde de parabole (en rouge ci-contre) ; le pied de la bissectrice décrit une torpille, le point de concours une strophoïde (en bleu clair ci-contre) , et le pied de la hauteur évidemment un cercle.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2008