Équation polaire : . Paramétrisation complexe : . Équation polaire dans le repère (A(a,0), ) : . Aire :  ; aire de la boucle intérieure : .

Le limaçon trisecteur est le lieu des points d'intersection de deux droites tournant chacune uniformément autour d'un point, l'une des droites ayant une vitesse égale à une fois et demi celle de l'autre (d'où le nom de sesquisectrice) ; c'est donc un cas particulier de sectrice de Maclaurin.

L'angle  est donc égal au 2/3 de , d'où l' on déduit la propriété de trisection : l'angle OMA est le tiers de l'angle BAM. Les inverses du limaçon trisecteur par rapport aux deux pôles A et B  à savoir l'hyperbole d'excentricité 2 et la trisectrice de Mac-Laurin, sont donc deux autres courbes trisectrices.

Comme son nom l'indique, le limaçon trisecteur est un limaçon de Pascal : c'est la conchoïde du cercle par rapport à son centre, avec un module égal à la moitié du rayon du cercle, et donc aussi une médiane polaire de deux cercles, ainsi qu'une podaire de cercle et une épitrochoïde :
 
 

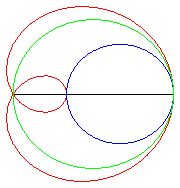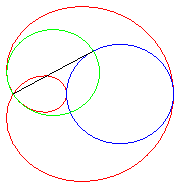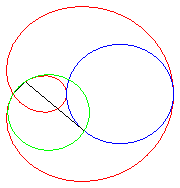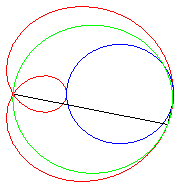
Limaçon trisecteur comme médiane polaire de deux cercles (donc aussi cissoïdale).	Limaçon trisecteur comme podaire de cercle.	Limaçon trisecteur comme épitrochoïde.	La paramétrisation complexe montre que le limaçon trisecteur est le lieu du mileu de deux points parcourant un cercle, l'un avec une vitesse double de l'autre.

Le limaçon trisecteur est aussi la podaire de la cardioïde par rapport au centre de son cercle conchoïdal.

La troisième équation ci-dessus montre enfin que c'est une rosace.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017