Polar equation: . Complex parametrization: . Polar equation in the frame (A(a,0), ): . Area: ; area of the interior loop: .

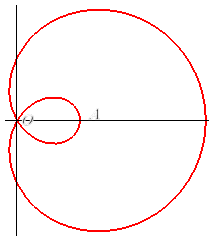The limaçon trisectrix is the locus of the intersection points between two lines, both turning uniformly around a point, the speed of one of which being 1.5 times the other's (hence the name of sesquisectrix); therefore, it is a special case of Maclaurin sectrix.

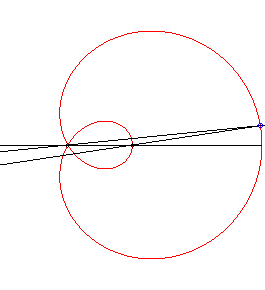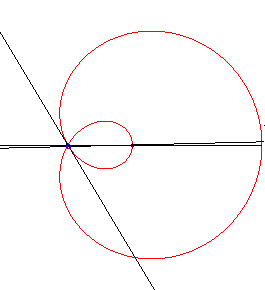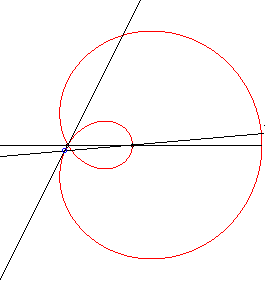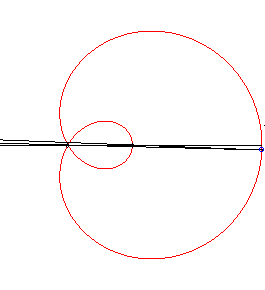The angle  is therefore equal to 2/3 of , from which we derive the trisection property: the angle OMA is the third of the angle BAM. The inverses of the  limaçon trisectrix with respect to the two poles A and B , namely the hyperbola with eccentricity 2 and the Mac-Laurin trisectrix, are therefore two other trisectrix curves.

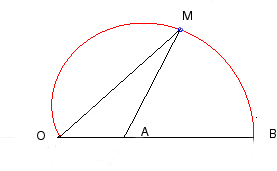As indicated by its name, the limaçon trisectrix is a limaçon of Pascal: it is the conchoid of the circle with respect to its centre, with a modulus equal to half the radius of the circle, and therefore also the polar median of two circles, as well as the pedal of a circle, and an epitrochoid:
 
 

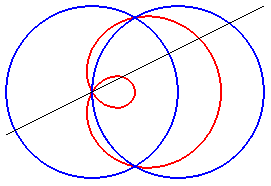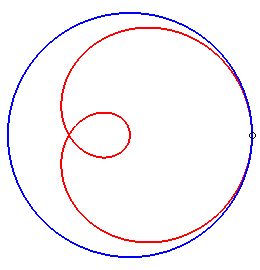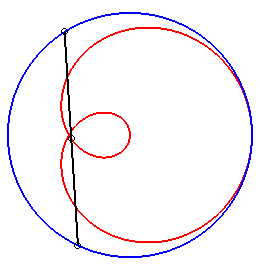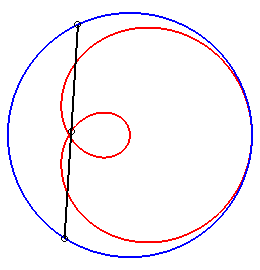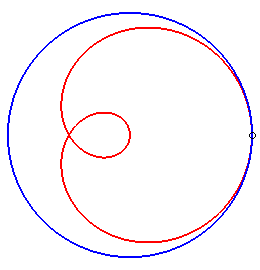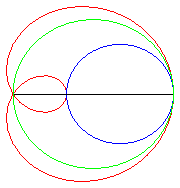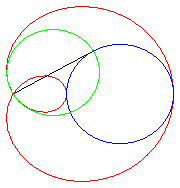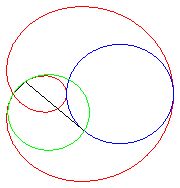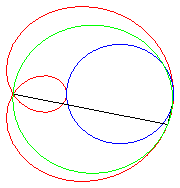
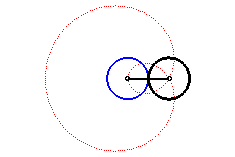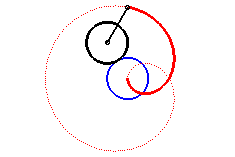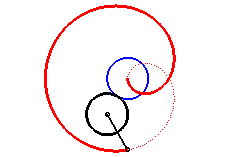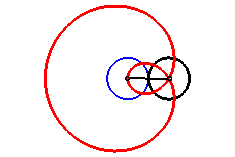
Trisectrix limaçon as the polar median of two circles (hence also a cissoid)	Trisectrix limaçon as the pedal of a circle.	Trisectrix limaçon as an epitrochoid.	The complex parametrization shows that the trisectrix limaçon is the locus of the middle of two points describing a circle, one of which going twice as fast as the other.

The limaçon trisectrix is also the pedal of the cardioid with respect to the centre of its conchoidal circle.

Finally, the third equation above shows that it is a rose.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017