Surface étudiée par Roberval et Torricelli en 1641. Gabriel : archange (trompettiste à ses heures...). Autres noms : cor de Gabriel, solide hyperbolique aigu (donné par Torricelli), entonnoir hyperbolique.

 

Équation cylindrique : . Equation cartésienne : . Surface quartique. Paramétrisation cartésienne : . Volume de la partie obtenue pour  : . Aire de cette partie : .

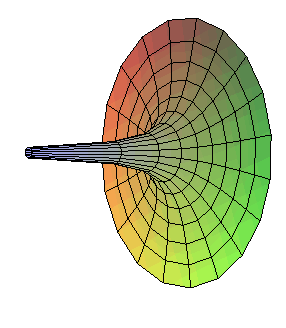
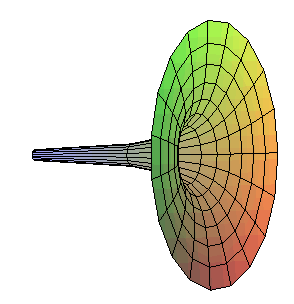
La trompette de Gabriel est la surface de révolution obtenue en faisant tourner une hyperbole équilatère autour de l’une de ses asymptotes.
Cette surface présente un paradoxe vraiment étonnant : si on veut remplir le tube (qui a une longueur infinie) formé par cette surface, il suffira d’une quantité finie de liquide, mais si on veut le peindre, il faudra une quantité infinie de peinture!
 

On peut résoudre ce paradoxe de la façon suivante : on suppose en fait que la couche de peinture a une épaisseur constante. Mais on peut très bien peindre la trompette avec une quantité finie de peinture en mettant une couche dont l'épaisseur tend vers 0 à l'infini. C'est justement ce qui se passerait si on remplissait l'intérieur de peinture !
 

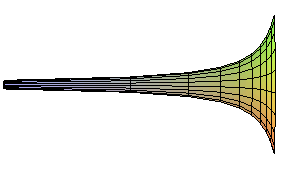
La surface assez proche de la précédente, d'équation cylindrique , se rencontre, elle, dans la vie courante, en particulier dans les cuisines ; c'est en effet la forme prise par un filet d'eau sortant d'un robinet à débit constant. On montre en effet que le rayon r du filet d'eau est donné en fonction de z (origine de l'axe à la sortie du robinet, axe dirigé vers le pas,  vitesse de l'eau à la sortie du robinet) par la formule .

Voir aussi le "Gabriel's cake", la tour à pression constante, et la seconde tractroïde.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2022