Gabriel's horn

GABRIEL'S HORN

Surface studied by Roberval and Torricelli in 1641.
Gabriel: archangel (and hornist in his spare time...).
Other name: acute hyperbolic solid (name given by Torricelli), hyperbolic funnel.

Cylindrical equation: .
Cartesian equation: .
Quartic surface.
Cartesian parametrization: .
Volume of the portion obtained for : .
Area of this portion: .

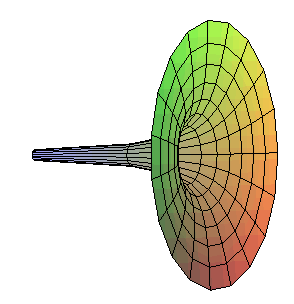
Gabriel's horn is the surface of revolution obtained by rotating a rectangular hyperbola around one of its asymptotes.
This surface displays a really surprising paradox: if we want to fill the tube formed by this surface (which has an infinite length), we will only need a finite amount of liquid, but if we want to paint it, we will need an infinite amount of paint!

This paradox can be solved in the following way: we are assuming that the layer of paint has a constant thickness. But we could very well paint the trumpet with a finite amount a paint and with the thickness of the layer going to 0 at infinity. This is precisely what would happen if we filled the inside with paint!

The surface, quite close to the previous one, with cylindrical equation , can be encountered in day-to-day life, especially in kitchens; it is indeed the shape assumed by a trickle of water coming out from a faucet with constant output.
Indeed, it can be proved that the radius r of the trickle of water is given as a function of z (the origin of the axis being at the faucet, the axis pointing downward, being the output speed of the water) by the formula .