TUBE or TUBULAR SURFACE or PIPE

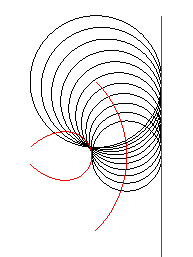
Tube with a horopter
curve as bore
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TUBE or TUBULAR SURFACE or PIPE

Tube with a horopter
curve as bore
| Synonyms: canal surface, channel surface. |
| Parametrization: Area of the section Volume of this section: |
The tubes with spine curve (or bore)
the curve
are the circled surfaces generated
by a circle with constant radius centered on
and the plane of which is always normal to this curve.
They are also the envelopes
of a sphere with constant radius centered on .
They are the Monge surfaces
with circular generatrix.
The visible
outline of a tube is composed of two parallel
curves of the projection of the spine curve.
Examples: the sphere (case where
is reduced to a point), the cylinder
of revolution, the torus, the
coil.
The notion can be generalized to three directions:
| 1) take a non circular section: we get the notion of Monge surface, with a closed generatrix: |
  |
| 2) take a circle with variable radius, still orthogonal
to the spine curve: we get the notion of tube with variable section.
Examples: - the surfaces of revolution - the sine tori of the second kind. |

Here is, for example, a tube the section of which varies sinusoidally. |
| 3) take spheres with variable radius centered
on When It is this general notion of envelope of spheres with variable radius that is sometimes referred to as "canal surface" [gray]. The characterization is: circled surface the circles of which are radii of curvature. Examples: the Dupin cyclides. |
  |
See also the solenoids,
coiling of a wire around a tube.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017